CF1679C Rooks Defenders
题目描述
你有一个 $n \times n$ 的正方形国际象棋棋盘。行从上到下编号为 $1$ 到 $n$,列从左到右编号为 $1$ 到 $n$。因此,每个格子用一对整数 $(x, y)$ 表示($1 \le x, y \le n$),其中 $x$ 表示行号,$y$ 表示列号。
你需要执行 $q$ 次操作,操作有三种类型:
- 在格子 $(x, y)$ 上放置一个新的车。
- 从格子 $(x, y)$ 上移除一个车。保证在当前操作前该格子上有车。
- 检查棋盘上子矩形 $(x_1, y_1)-(x_2, y_2)$ 内的每个格子是否都被至少一个车攻击。
子矩形是指所有满足 $x_1 \le x \le x_2$ 且 $y_1 \le y \le y_2$ 的格子 $(x, y)$ 的集合。
回忆一下,如果在 $(c, d)$ 放置一个车,则格子 $(a, b)$ 会被该车攻击,当且仅当 $a = c$ 或 $b = d$。特别地,包含车本身的格子也会被该车攻击。
输入格式
第一行包含两个整数 $n$ 和 $q$($1 \le n \le 10^5$,$1 \le q \le 2 \times 10^5$),分别表示棋盘的大小和操作的数量。
接下来的 $q$ 行,每行描述一个操作。每个操作以一个整数 $t$($t \in \{1, 2, 3\}$)开头,表示操作类型:
- 如果 $t = 1$,接下来有两个整数 $x$ 和 $y$($1 \le x, y \le n$),表示在 $(x, y)$ 放置一个新的车。保证当前该格子上没有车。
- 如果 $t = 2$,接下来有两个整数 $x$ 和 $y$($1 \le x, y \le n$),表示从 $(x, y)$ 移除一个车。保证当前该格子上有车。
- 如果 $t = 3$,接下来有四个整数 $x_1, y_1, x_2, y_2$($1 \le x_1 \le x_2 \le n$,$1 \le y_1 \le y_2 \le n$),表示需要检查子矩形 $(x_1, y_1)-(x_2, y_2)$ 内的每个格子是否都被至少一个车攻击。
保证在 $q$ 个操作中至少有一个为第三类操作。
输出格式
对于每个第三类操作,输出一行答案。如果子矩形内每个格子都被至少一个车攻击,输出 "Yes"(不带引号);否则输出 "No"(不带引号)。
说明/提示
请参考示例。前两次操作后,棋盘如下图所示(字母 $R$ 表示有车的格子,绿色高亮部分为第三类操作的子矩形):

执行第三和第四次操作后的棋盘:
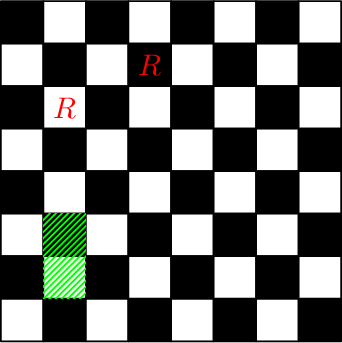
执行第五和第六次操作后的棋盘:
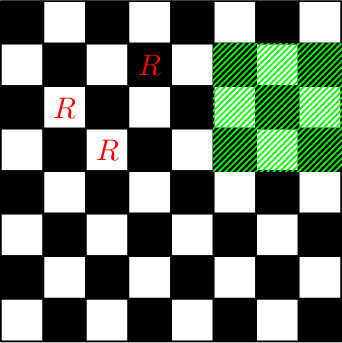
执行第七和第八次操作后的棋盘:

执行最后两次操作后的棋盘:

由 ChatGPT 4.1 翻译