CF1679D Toss a Coin to Your Graph...

One day Masha was walking in the park and found a graph under a tree... Surprised? Did you think that this problem would have some logical and reasoned story? No way! So, the problem... Masha has an oriented graph which $ i $ -th vertex contains some positive integer $ a_i $ . Initially Masha can put a coin at some vertex. In one operation she can move a coin placed in some vertex $ u $ to any other vertex $ v $ such that there is an oriented edge $ u \to v $ in the graph. Each time when the coin is placed in some vertex $ i $ , Masha write down an integer $ a_i $ in her notebook (in particular, when Masha initially puts a coin at some vertex, she writes an integer written at this vertex in her notebook). Masha wants to make exactly $ k - 1 $ operations in such way that the maximum number written in her notebook is as small as possible.

The first line contains three integers $ n $ , $ m $ and $ k $ ( $ 1 \le n \le 2 \cdot 10^5 $ , $ 0 \le m \le 2 \cdot 10^5 $ , $ 1 \le k \le 10^{18} $ ) — the number of vertices and edges in the graph, and the number of operation that Masha should make. The second line contains $ n $ integers $ a_i $ ( $ 1 \le a_i \le 10^9 $ ) — the numbers written in graph vertices. Each of the following $ m $ lines contains two integers $ u $ and $ v $ ( $ 1 \le u \ne v \le n $ ) — it means that there is an edge $ u \to v $ in the graph. It's guaranteed that graph doesn't contain loops and multi-edges.

Print one integer — the minimum value of the maximum number that Masha wrote in her notebook during optimal coin movements. If Masha won't be able to perform $ k - 1 $ operations, print $ -1 $ .

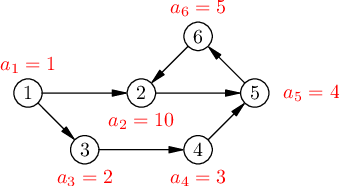Graph described in the first and the second examples is illustrated below. In the first example Masha can initially put a coin at vertex $ 1 $ . After that she can perform three operations: $ 1 \to 3 $ , $ 3 \to 4 $ and $ 4 \to 5 $ . Integers $ 1, 2, 3 $ and $ 4 $ will be written in the notepad. In the second example Masha can initially put a coin at vertex $ 2 $ . After that she can perform $ 99 $ operations: $ 2 \to 5 $ , $ 5 \to 6 $ , $ 6 \to 2 $ , $ 2 \to 5 $ , and so on. Integers $ 10, 4, 5, 10, 4, 5, \ldots, 10, 4, 5, 10 $ will be written in the notepad. In the third example Masha won't be able to perform $ 4 $ operations.