CF167D Wizards and Roads

在某个国家里住着一些巫师。他们喜欢建造城市和道路。 这个国家以前有 $k$ 个城市，第 $j$ 个城市（$1\leq j \leq k$）位于点 $(x_j, y_j)$。现在决定再新建 $n-k$ 个城市。对于第 $i$ 个新城市（$k < i \leq n$），其坐标 $(x_i, y_i)$ 按如下方式生成： - $x_{i}=(a \cdot x_{i-1}+b)\bmod (10^{9}+9)$ - $y_{i}=(c \cdot y_{i-1}+d)\bmod (10^{9}+9)$ 其中 $a$、$b$、$c$、$d$ 都是质数，且 $a \neq c, b \neq d$。 在所有 $n$ 个城市建好后，巫师们惊讶地发现，对于任意两个不同的城市 $i$ 和 $j$，总有 $x_i \neq x_j$ 且 $y_i \neq y_j$。 城市建好后，接下来就是修路了！他们决定使用最困难（当然也是最强大）的魔法来修路。使用这种魔法能在第 $u$ 城与第 $v$ 城之间建一条路（$y_u>y_v$），当且仅当对于每一个严格位于 $u,v$ 构成的“角”内部的城市 $w$，都存在一个不位于“角”内部的城市 $s$，满足其 $x$ 坐标严格在 $w$ 和 $u$ 之间，并且 $y_s > y_v$。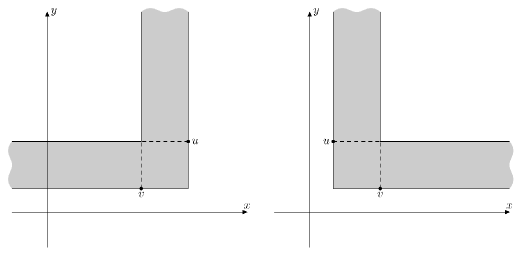 对于点 $p_2 (x_2, y_2)$、$p_1 (x_1, y_1)$（$y_1 < y_2$），“角”定义为满足以下至少一个条件的所有点 $(x, y)$ 的集合： - $\min(x_1, x_2) \leq x \leq \max(x_1, x_2)$ 且 $y \geq y_1$ - $y_1 \leq y \leq y_2$ 且 $(x-x_2)\cdot(x_1-x_2) \geq 0$  如图所示，两种不同“角”的示意图。 为了测试魔法，巫师们将在所有 $x$ 坐标属于 $[L,R]$ 区间的城市之间施展此法术。道路建成后，政府想要选择最多数目的配对（每对城市之间有道路连接，并且每个城市至多属于一对），即最大匹配。请你对于每个给定的 $L$、$R$ 查询，求最大可配对的数量。注意，不在 $[L,R]$ 区间的城市对建路毫无影响。

第一行两个用空格分隔的整数 $n, k$（$1\leq k\leq n\leq 10^5$，$k\leq 30$）。接下来的 $k$ 行，每行包含两个整数 $x_j, y_j$（$0 \leq x_j, y_j < 10^9+9$），表示第 $j$ 个城市的坐标。 下一行四个用空格分隔的整数 $a, b, c, d$（$2\leq a, b, c, d < 10^9+9$）。保证这些数字都为质数，且 $a \neq c, b \neq d$。 保证任意两个城市 $i, j$，都有 $x_i \neq x_j$ 且 $y_i \neq y_j$。 接下来一行一个整数 $m$（$1\leq m\leq 10^5$），表示建路方案的个数。接下来的 $m$ 行，每行两个整数 $L_i, R_i$（$0 \leq L_i \leq R_i < 10^9+9$），表示第 $i$ 组查询的 $L$、$R$。

对于每一组 $L_i, R_i$，输出一个答案，占一行。按输入顺序输出。

在第一个样例中，道路将城市按 $x$ 从小到大连接成一条链。 在第二个样例中，额外 5 个城市分别位于 $(5, 11)$、$(20, 263098)$、$(65, 292514823)$、$(200, 76958738)$、$(605, 622120197)$。 由 ChatGPT 5 翻译