CF1680F Lenient Vertex Cover

You are given a simple connected undirected graph, consisting of $ n $ vertices and $ m $ edges. The vertices are numbered from $ 1 $ to $ n $ . A vertex cover of a graph is a set of vertices such that each edge has at least one of its endpoints in the set. Let's call a lenient vertex cover such a vertex cover that at most one edge in it has both endpoints in the set. Find a lenient vertex cover of a graph or report that there is none. If there are multiple answers, then print any of them.

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of testcases. The first line of each testcase contains two integers $ n $ and $ m $ ( $ 2 \le n \le 10^6 $ ; $ n - 1 \le m \le \min(10^6, \frac{n \cdot (n - 1)}{2}) $ ) — the number of vertices and the number of edges of the graph. Each of the next $ m $ lines contains two integers $ v $ and $ u $ ( $ 1 \le v, u \le n $ ; $ v \neq u $ ) — the descriptions of the edges. For each testcase, the graph is connected and doesn't have multiple edges. The sum of $ n $ over all testcases doesn't exceed $ 10^6 $ . The sum of $ m $ over all testcases doesn't exceed $ 10^6 $ .

For each testcase, the first line should contain YES if a lenient vertex cover exists, and NO otherwise. If it exists, the second line should contain a binary string $ s $ of length $ n $ , where $ s_i = 1 $ means that vertex $ i $ is in the vertex cover, and $ s_i = 0 $ means that vertex $ i $ isn't. If there are multiple answers, then print any of them.

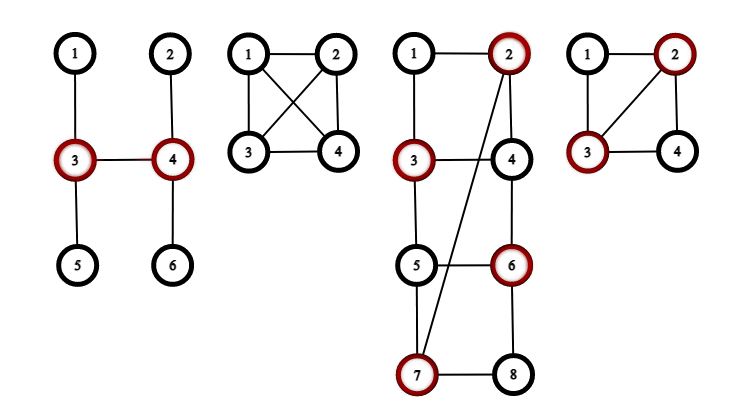
Here are the graphs from the first example. The vertices in the lenient vertex covers are marked red.