CF1681E Labyrinth Adventures
题目描述
有一个 $n\times n$ 的方格图,坐标编号类似平面直角坐标系,左下角为 $(1, 1)$。
这个方格图被分成了 $n$ 层,左下角 $(1, 1)$ 为第一层,随后每层都向外拓展一圈,如下图就是 $n=5$ 的时候的情况:
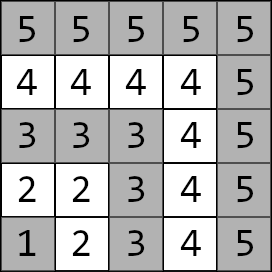
层与层之间有墙隔开,但每层都有两个门,分别分布在该层顶部和右侧,门是双向的。
现在给出这些门的坐标,有 $m$ 次询问,每次给定两个坐标 $(x_1, y_1)$ 和 $(x_2,y_2)$,请你回答两点之间的最短路。
输入格式
第一行输入 $n$。
接下来的 $n-1$ 行中,每行有四个整数 $d_{1,x}, d_{1,y}, d_{2,x}, d_{2,y}$,表示第 $i$ 层的两个门的坐标。前两个表示顶部门坐标,后两个表示右侧门坐标。
之后一行输入 $m$。
接下来的 $m$ 行中,每行有四个整数 $x_1,y_1,x_2,y_2$,表示每次询问中起点与终点的坐标。
输出格式
对每次询问,输出一行一个整数,表示两点之间的最短路长度。**长度的定义是移动的步数。**
#### 样例解释
下图是样例二的网格图,红色的是门。
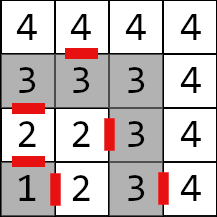
说明/提示
$1 \le n \le 10^5$;
$2 \le m \le 2 \times 10^5$。