CF1682D Circular Spanning Tree

有 $n$ 个节点按顺时针顺序排列成一个圆圈，编号为 $1$ 到 $n$。你还得到一个长度为 $n$ 的二进制字符串 $s$。 你的任务是，在这 $n$ 个节点上构造一棵满足以下两个条件的树，或者报告不存在这样的树： - 对于每个节点 $i$（$1 \leq i \leq n$），如果 $s_i = 0$，则该节点的度数为偶数；如果 $s_i = 1$，则该节点的度数为奇数。 - 在圆圈内部，树的任意两条边都不能有内部交点。允许边在圆周上相交。 注意，所有边都画为直线段。例如，树中的边 $(u, v)$ 画为连接圆圈上 $u$ 和 $v$ 的线段。 一棵 $n$ 个节点的树是一个连通且有 $n-1$ 条边的图。

输入包含多组测试用例。第一行包含一个整数 $t$（$1 \leq t \leq 2 \cdot 10^4$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 2 \cdot 10^5$），表示节点数。 第二行包含一个长度为 $n$ 的二进制字符串 $s$。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，如果不存在满足条件的树，则输出 "NO"（不带引号）；否则输出 "YES"，并输出该树的描述。 你可以以任意大小写输出每个字母（例如 "YES"、"Yes"、"yes"、"yEs" 都会被识别为肯定答案）。 如果存在这样的树，则输出 $n-1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \leq u, v \leq n, u \neq v$），表示树中的一条边。如果有多种方案，输出任意一种即可。

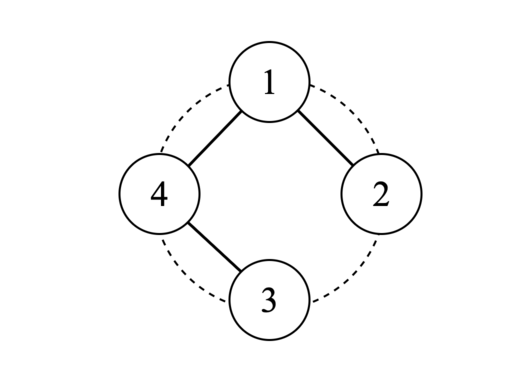
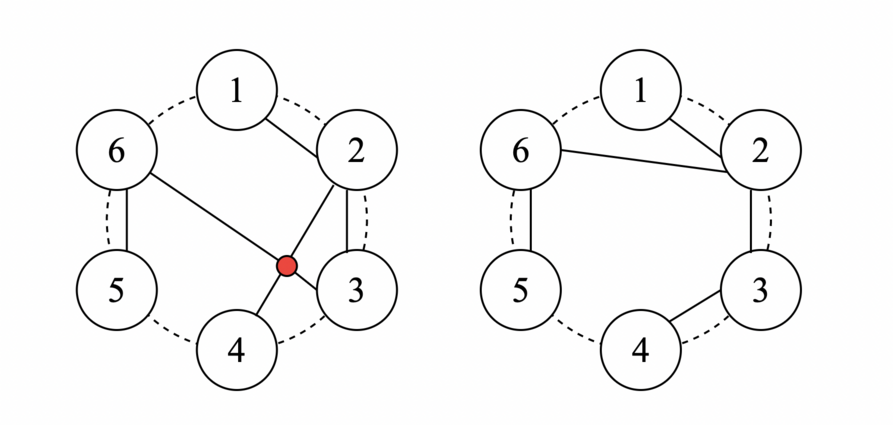
在第一个测试用例中，树如下图所示：  在第二个测试用例中，唯一可能的树是连接 $1$ 和 $2$ 的一条边，但它不满足度数限制。 在第三个测试用例中，  左侧的树满足度数限制，但边在圆内部有交点，因此不是合法的树；右侧的树是合法的。 由 ChatGPT 4.1 翻译