CF1682F MCMF?

给定两个整数数组 $a$ 和 $b$（$b_i \neq 0$ 且 $|b_i| \leq 10^9$）。数组 $a$ 已按非递减顺序排序。 定义子数组 $a[l:r]$ 的代价如下： - 如果 $ \sum\limits_{j = l}^{r} b_j \neq 0 $，则该子数组的代价未定义。 - 否则： - 构建一个二分图流网络，包含 $r-l+1$ 个顶点，编号为 $l$ 到 $r$，所有 $b_i0$ 的顶点在右侧。对于每一对 $i, j$ 满足 $l \leq i, j \leq r$，$b_i0$，从 $i$ 向 $j$ 连一条容量为无穷大、单位流量费用为 $|a_i-a_j|$ 的边。 - 再添加两个顶点：源点 $S$ 和汇点 $T$。 - 对于每个 $l \leq i \leq r$ 且 $b_i0$，从 $i$ 向 $T$ 连一条容量为 $|b_i|$、费用为 $0$ 的边。 - 子数组的代价定义为从 $S$ 到 $T$ 的最大流的最小费用。 你将会得到 $q$ 个询问，每个询问给出两个整数 $l$ 和 $r$。你需要计算每个询问对应的子数组 $a[l:r]$ 的代价，结果对 $10^9+7$ 取模。 如果你不了解最小费用最大流的含义，可以阅读[这里](https://en.wikipedia.org/wiki/Minimum-cost_flow_problem)。

输入的第一行包含两个整数 $n$ 和 $q$（$2 \leq n \leq 2\cdot 10^5, 1 \leq q \leq 2\cdot10^5$）——数组 $a$、$b$ 的长度和询问的数量。 第二行包含 $n$ 个整数 $a_1,a_2,\ldots,a_n$（$0 \leq a_1 \leq a_2 \leq \ldots \leq a_n \leq 10^9$）——数组 $a$。保证 $a$ 已按非递减顺序排序。 第三行包含 $n$ 个整数 $b_1,b_2,\ldots,b_n$（$-10^9\leq b_i \leq 10^9, b_i \neq 0$）——数组 $b$。 接下来 $q$ 行，每行包含两个整数 $l_i,r_i$（$1\leq l_i \leq r_i \leq n$）。保证 $ \sum\limits_{j = l_i}^{r_i} b_j = 0 $。

对于每个询问 $l_i, r_i$，输出子数组 $a[l_i:r_i]$ 的代价，对 $10^9+7$ 取模。

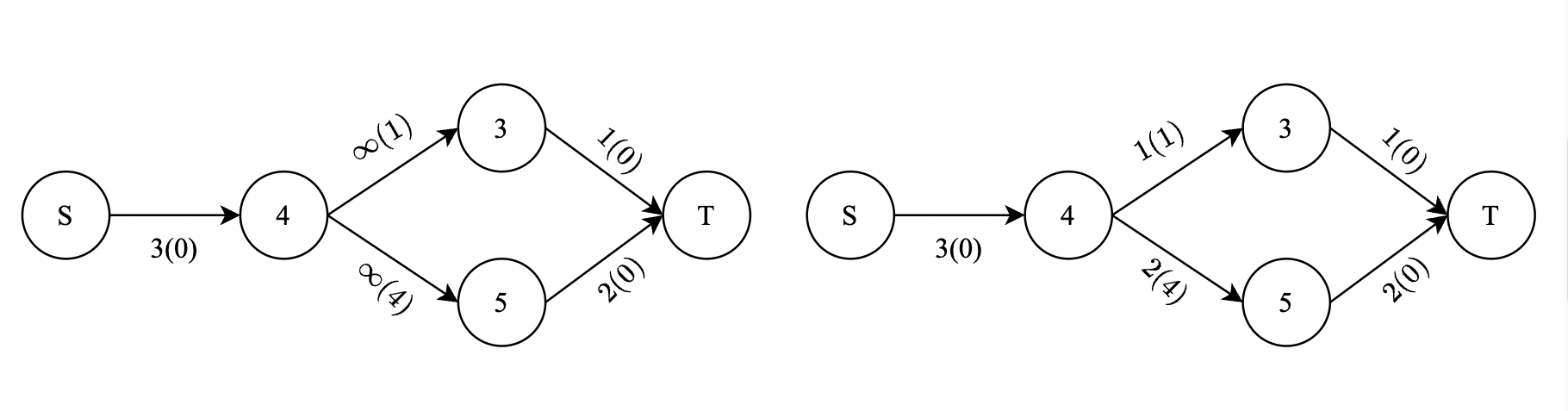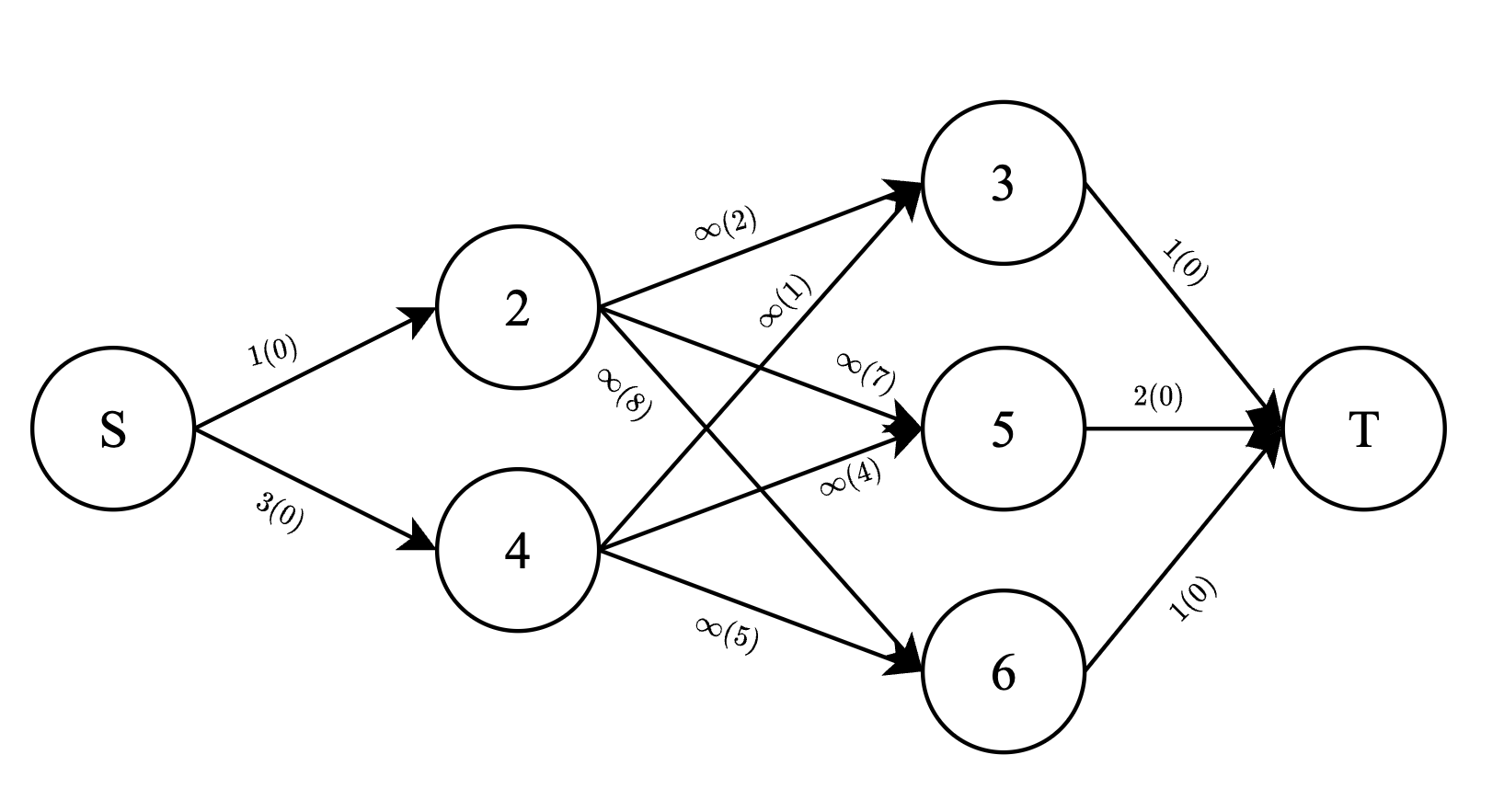
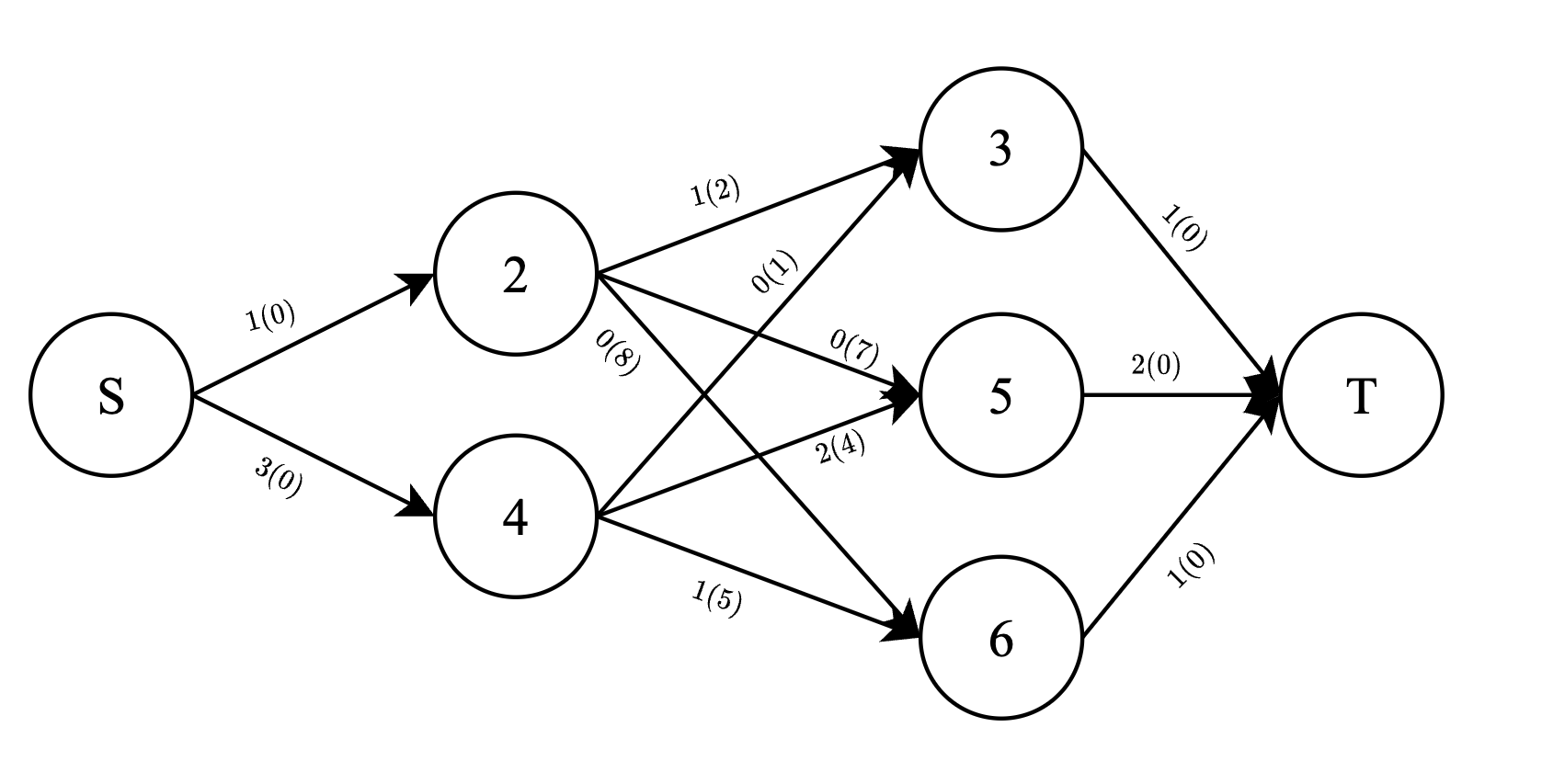
在第一个询问中，最大可能流量为 $1$，即从源点到 $2$，再从 $2$ 到 $3$，最后从 $3$ 到汇点，流量均为 $1$。流量的总代价为 $0 \cdot 1 + |2 - 4| \cdot 1 + 0 \cdot 1 = 2$。 在第二个询问中，最大可能流量仍为 $1$，即从源点到 $7$，$7$ 到 $6$，$6$ 到汇点，总代价为 $0 \cdot |10 - 10| \cdot 1 + 0 \cdot 1 = 0$。 在第三个询问中，流网络如左图所示，边上标注了容量，括号内为费用。右图展示了最优流量分配。  最大流量为 $3$，总代价为 $0 \cdot 3 + 1 \cdot 1 + 4 \cdot 2 + 0 \cdot 1 + 0 \cdot 2 = 9$。 在第四个询问中，流网络如下所示——  最小费用最大流的最优分配如下——  上述网络的最大流量为 $4$，最小费用为 $15$。 由 ChatGPT 4.1 翻译