CF1690A Print a Pedestal (Codeforces logo?)

Given the integer $ n $ — the number of available blocks. You must use all blocks to build a pedestal. The pedestal consists of $ 3 $ platforms for $ 2 $ -nd, $ 1 $ -st and $ 3 $ -rd places respectively. The platform for the $ 1 $ -st place must be strictly higher than for the $ 2 $ -nd place, and the platform for the $ 2 $ -nd place must be strictly higher than for the $ 3 $ -rd place. Also, the height of each platform must be greater than zero (that is, each platform must contain at least one block). 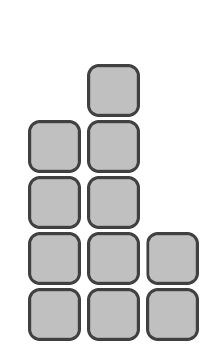Example pedestal of $ n=11 $ blocks: second place height equals $ 4 $ blocks, first place height equals $ 5 $ blocks, third place height equals $ 2 $ blocks.Among all possible pedestals of $ n $ blocks, deduce one such that the platform height for the $ 1 $ -st place minimum as possible. If there are several of them, output any of them.

The first line of input data contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. Each test case contains a single integer $ n $ ( $ 6 \le n \le 10^5 $ ) — the total number of blocks for the pedestal. All $ n $ blocks must be used. It is guaranteed that the sum of $ n $ values over all test cases does not exceed $ 10^6 $ .

For each test case, output $ 3 $ numbers $ h_2, h_1, h_3 $ — the platform heights for $ 2 $ -nd, $ 1 $ -st and $ 3 $ -rd places on a pedestal consisting of $ n $ blocks ( $ h_1+h_2+h_3=n $ , $ 0 < h_3 < h_2 < h_1 $ ). Among all possible pedestals, output the one for which the value of $ h_1 $ minimal. If there are several of them, output any of them.

In the first test case we can not get the height of the platform for the first place less than $ 5 $ , because if the height of the platform for the first place is not more than $ 4 $ , then we can use at most $ 4 + 3 + 2 = 9 $ blocks. And we should use $ 11 = 4 + 5 + 2 $ blocks. Therefore, the answer 4 5 2 fits. In the second set, the only suitable answer is: 2 3 1.