CF1691F K-Set Tree

给定一棵有 $n$ 个顶点的树 $G$ 和一个整数 $k$。树的顶点编号为 $1$ 到 $n$。 对于一个顶点 $r$ 和树中顶点的一个子集 $S$，其中 $|S| = k$，我们定义 $f(r, S)$ 为以 $r$ 为根时，包含 $S$ 中所有顶点的最小有根子树的大小。一个顶点集合 $T$ 被称为有根子树，当且仅当 $T$ 中所有顶点连通，且对于 $T$ 中的每个顶点，其所有后代也都属于 $T$。 你需要计算所有可能的不同顶点 $r$ 和子集 $S$（$|S| = k$）的 $f(r, S)$ 之和。形式化地，计算如下表达式： $$ \sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S) $$ 其中 $V$ 是树 $G$ 的顶点集合。 请将答案对 $10^9 + 7$ 取模后输出。

第一行包含两个整数 $n$ 和 $k$（$3 \le n \le 2 \cdot 10^5$，$1 \le k \le n$）。 接下来的 $n-1$ 行，每行包含两个整数 $x$ 和 $y$（$1 \le x, y \le n$），表示顶点 $x$ 和 $y$ 之间有一条边。 保证给定的边构成一棵树。

输出答案对 $10^9 + 7$ 取模后的结果。

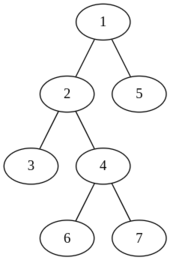
第二个样例中的树如下图所示：  在该树中，大小为 $2$ 的子集共有 $21$ 个，即 $$ S \in \left\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\} \right\} $$ 并且由于有 $7$ 个顶点，$1 \le r \le 7$。我们需要对所有可能的 $r$ 和 $S$ 组合，计算 $f(r, S)$ 的总和。 下面列出了一些 $r$ 和 $S$ 组合对应的 $f(r, S)$ 值： - $r = 1$，$S = \{3, 7\}$。此时 $f(r, S) = 5$，对应的子树为 $\{2, 3, 4, 6, 7\}$。 - $r = 1$，$S = \{5, 4\}$。此时 $f(r, S) = 7$，对应的子树为 $\{1, 2, 3, 4, 5, 6, 7\}$。 - $r = 1$，$S = \{4, 6\}$。此时 $f(r, S) = 3$，对应的子树为 $\{4, 6, 7\}$。 由 ChatGPT 4.1 翻译