CF1691F K-Set Tree

You are given a tree $ G $ with $ n $ vertices and an integer $ k $ . The vertices of the tree are numbered from $ 1 $ to $ n $ . For a vertex $ r $ and a subset $ S $ of vertices of $ G $ , such that $ |S| = k $ , we define $ f(r, S) $ as the size of the smallest rooted subtree containing all vertices in $ S $ when the tree is rooted at $ r $ . A set of vertices $ T $ is called a rooted subtree, if all the vertices in $ T $ are connected, and for each vertex in $ T $ , all its descendants belong to $ T $ . You need to calculate the sum of $ f(r, S) $ over all possible distinct combinations of vertices $ r $ and subsets $ S $ , where $ |S| = k $ . Formally, compute the following: $ $$$\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S), $ $ where $ V $ is the set of vertices in $ G $ .

Output the answer modulo $ 10^9 + 7$$$.

The first line contains two integers $ n $ and $ k $ ( $ 3 \le n \le 2 \cdot 10^5 $ , $ 1 \le k \le n $ ). Each of the following $ n - 1 $ lines contains two integers $ x $ and $ y $ ( $ 1 \le x, y \le n $ ), denoting an edge between vertex $ x $ and $ y $ . It is guaranteed that the given edges form a tree.

Print the answer modulo $ 10^9 + 7 $ .

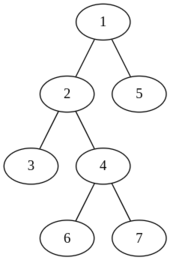The tree in the second example is given below: We have $ 21 $ subsets of size $ 2 $ in the given tree. Hence, $ $$$S \in \left\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\} \right\}. $ $ And since we have $ 7 $ vertices, $ 1 \\le r \\le 7 $ . We need to find the sum of $ f(r, S) $ over all possible pairs of $ r $ and $ S $ .

Below we have listed the value of $ f(r, S) $ for some combinations of $ r $ and $ S $ .

• $ r = 1 $ , $ S = \\{3, 7\\} $ . The value of $ f(r, S) $ is $ 5 $ and the corresponding subtree is $ \\{2, 3, 4, 6, 7\\} $ .
• $ r = 1 $ , $ S = \\{5, 4\\} $ . The value of $ f(r, S) $ is $ 7 $ and the corresponding subtree is $ \\{1, 2, 3, 4, 5, 6, 7\\} $ .
• $ r = 1 $ , $ S = \\{4, 6\\} $ . The value of $ f(r, S) $ is $ 3 $ and the corresponding subtree is $ \\{4, 6, 7\\}$$$.