CF1695C Zero Path

给定一个有 $n$ 行 $m$ 列的网格。我们用 $(i, j)$ 表示第 $i$ 行（$1\le i\le n$）、第 $j$ 列（$1\le j\le m$）的格子，该格子的数值为 $a_{ij}$。所有的数值均为 $1$ 或 $-1$。 你从格子 $(1, 1)$ 出发，每次可以向下或向右移动一格。最终你需要到达格子 $(n, m)$。 是否存在一种移动方式，使得经过的所有格子的数值之和（包括 $a_{11}$ 和 $a_{nm}$）恰好为 $0$？ 

每组测试数据包含多组测试用例。第一行包含一个整数 $t$（$1 \leq t \leq 10^4$），表示测试用例的数量。 每组测试用例的第一行包含两个整数 $n$ 和 $m$（$1 \le n, m \le 1000$），表示网格的大小。 接下来的 $n$ 行，每行包含 $m$ 个整数。第 $i$ 行第 $j$ 个整数为 $a_{ij}$（$a_{ij} = 1$ 或 $-1$），表示格子 $(i, j)$ 的数值。 保证所有测试用例中 $n\cdot m$ 的总和不超过 $10^6$。

对于每组测试用例，如果存在一条从左上角到右下角的路径，使得经过的所有格子的数值之和为 $0$，输出 "YES"；否则输出 "NO"。输出时字母大小写均可。

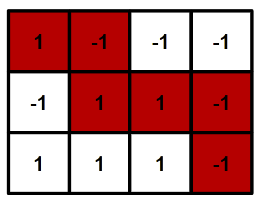
第四组测试用例的一个可行路径如题面图片所示。 由 ChatGPT 4.1 翻译