CF1695C Zero Path
Description
You are given a grid with $ n $ rows and $ m $ columns. We denote the square on the $ i $ -th ( $ 1\le i\le n $ ) row and $ j $ -th ( $ 1\le j\le m $ ) column by $ (i, j) $ and the number there by $ a_{ij} $ . All numbers are equal to $ 1 $ or to $ -1 $ .
You start from the square $ (1, 1) $ and can move one square down or one square to the right at a time. In the end, you want to end up at the square $ (n, m) $ .
Is it possible to move in such a way so that the sum of the values written in all the visited cells (including $ a_{11} $ and $ a_{nm} $ ) is $ 0 $ ?
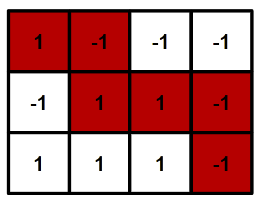
Input Format
Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \leq t \leq 10^4 $ ). Description of the test cases follows.
The first line of each test case contains two integers $ n $ and $ m $ ( $ 1 \le n, m \le 1000 $ ) — the size of the grid.
Each of the following $ n $ lines contains $ m $ integers. The $ j $ -th integer on the $ i $ -th line is $ a_{ij} $ ( $ a_{ij} = 1 $ or $ -1 $ ) — the element in the cell $ (i, j) $ .
It is guaranteed that the sum of $ n\cdot m $ over all test cases does not exceed $ 10^6 $ .
Output Format
For each test case, print "YES" if there exists a path from the top left to the bottom right that adds up to $ 0 $ , and "NO" otherwise. You can output each letter in any case.
Explanation/Hint
One possible path for the fourth test case is given in the picture in the statement.