Permutation Graph

### 题目描述 给出一个 $1$ 到 $n$ 的排列 $ [a_1,a_2,\dots,a_n] $ 。对于 $1\le i < j\le n$ ，记 $ \operatorname{mn}(i,j) $ 为 $\min\limits_{k=i}^j a_k$ ，记 $ \operatorname{mx}(i,j) $ 为 $ \max\limits_{k=i}^j a_k $ 。 有一张 $n$ 个点的无向图，点的编号为 $1$ 到 $n$ 。对于每一对整数 $ 1\le i<j\le n $ ，如果同时满足 $ \operatorname{mn}(i,j)=a_i $ 且 $ \operatorname{mx}(i,j)=a_j $ ，或同时满足 $ \operatorname{mn}(i,j)=a_j $ 和 $ \operatorname{mx}(i,j)=a_i $ ，那么就在 $i$ 和 $j$ 之间连一条长度为 $1$ 的边。 询问这张图中从 $1$ 到 $n$ 的最短路的长度。可以证明 $1$ 和 $n$ 总是连通，所以最短路总是存在。 ### 输入格式 每个数据点包含多组数据。第一行一个整数 $t$ ( $ 1 \le t \le 5\cdot 10^4 $ ) 表示测试组数 对于每组数据，第一行一个整数 $n$ ( $ 1\le n\le 2.5\cdot 10^5 $ ) 。 第二行包含 $n$ 个整数 $ a_1 $ , $ a_2 $ , $ \ldots $ , $ a_n $ ( $ 1\le a_i\le n $ ) 。保证 $a$ 是 $ 1 $ , $ 2 $ , $ \dots $ , $ n $ 的一个排列。 保证所有数据的 $n$ 之和不超过 $ 5\cdot 10^5 $ ### 输出格式 对于每组数据，输出一个整数表示从 $1$ 到 $n$ 的最短路长度

A permutation is an array consisting of $ n $ distinct integers from $ 1 $ to $ n $ in arbitrary order. For example, $ [2,3,1,5,4] $ is a permutation, but $ [1,2,2] $ is not a permutation ( $ 2 $ appears twice in the array) and $ [1,3,4] $ is also not a permutation ( $ n=3 $ but there is $ 4 $ in the array). You are given a permutation of $ 1,2,\dots,n $ , $ [a_1,a_2,\dots,a_n] $ . For integers $ i $ , $ j $ such that $ 1\le i<j\le n $ , define $ \operatorname{mn}(i,j) $ as $ \min\limits_{k=i}^j a_k $ , and define $ \operatorname{mx}(i,j) $ as $ \max\limits_{k=i}^j a_k $ . Let us build an undirected graph of $ n $ vertices, numbered $ 1 $ to $ n $ . For every pair of integers $ 1\le i<j\le n $ , if $ \operatorname{mn}(i,j)=a_i $ and $ \operatorname{mx}(i,j)=a_j $ both holds, or $ \operatorname{mn}(i,j)=a_j $ and $ \operatorname{mx}(i,j)=a_i $ both holds, add an undirected edge of length $ 1 $ between vertices $ i $ and $ j $ . In this graph, find the length of the shortest path from vertex $ 1 $ to vertex $ n $ . We can prove that $ 1 $ and $ n $ will always be connected via some path, so a shortest path always exists.

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 5\cdot 10^4 $ ). Description of the test cases follows. The first line of each test case contains one integer $ n $ ( $ 1\le n\le 2.5\cdot 10^5 $ ). The second line of each test case contains $ n $ integers $ a_1 $ , $ a_2 $ , $ \ldots $ , $ a_n $ ( $ 1\le a_i\le n $ ). It's guaranteed that $ a $ is a permutation of $ 1 $ , $ 2 $ , $ \dots $ , $ n $ . It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 5\cdot 10^5 $ .

For each test case, print a single line containing one integer — the length of the shortest path from $ 1 $ to $ n $ .

5
1
1
2
1 2
5
1 4 2 3 5
5
2 1 5 3 4
10
7 4 8 1 6 10 3 5 2 9

0
1
1
4
6

The following are illustrations of constructed graphs in example test cases. the constructed graph in test case 1 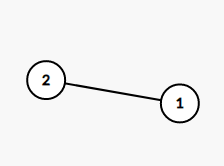the constructed graph in test case 2 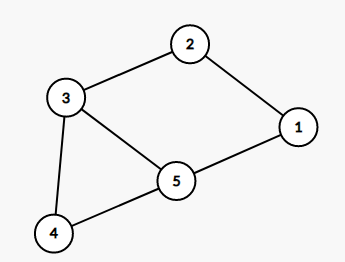the constructed graph in test case 3 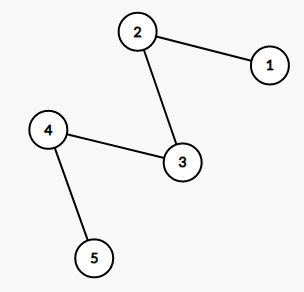the constructed graph in test case 4 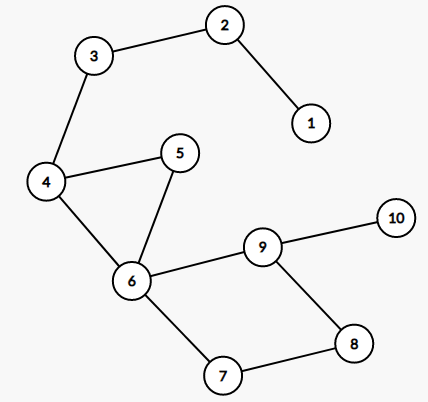the constructed graph in test case 5