CF1696D Permutation Graph

A permutation is an array consisting of $ n $ distinct integers from $ 1 $ to $ n $ in arbitrary order. For example, $ [2,3,1,5,4] $ is a permutation, but $ [1,2,2] $ is not a permutation ( $ 2 $ appears twice in the array) and $ [1,3,4] $ is also not a permutation ( $ n=3 $ but there is $ 4 $ in the array). You are given a permutation of $ 1,2,\dots,n $ , $ [a_1,a_2,\dots,a_n] $ . For integers $ i $ , $ j $ such that $ 1\le i

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 5\cdot 10^4 $ ). Description of the test cases follows. The first line of each test case contains one integer $ n $ ( $ 1\le n\le 2.5\cdot 10^5 $ ). The second line of each test case contains $ n $ integers $ a_1 $ , $ a_2 $ , $ \ldots $ , $ a_n $ ( $ 1\le a_i\le n $ ). It's guaranteed that $ a $ is a permutation of $ 1 $ , $ 2 $ , $ \dots $ , $ n $ . It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 5\cdot 10^5 $ .

For each test case, print a single line containing one integer — the length of the shortest path from $ 1 $ to $ n $ .

The following are illustrations of constructed graphs in example test cases. the constructed graph in test case 1 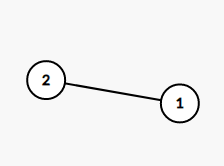the constructed graph in test case 2 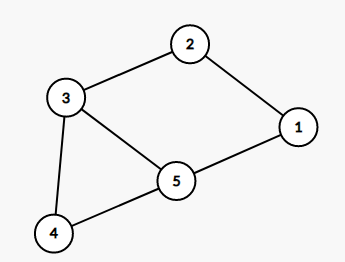the constructed graph in test case 3 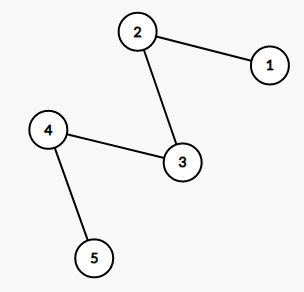the constructed graph in test case 4 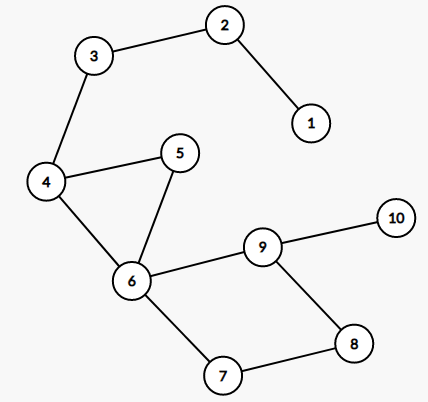the constructed graph in test case 5