CF1700A Optimal Path

# 最优路径 你得到一个大小为 $ n \times m $ 的表 $ a $ 。我们将考虑从上到下从 $1$ 到 $n$ 编号的表格行，从左到右从 $1$ 到 $m$ 编号的列。我们将在 $ i $ -th 行和 $ j $ -th 列中的单元格表示为 $ (i, j) $ 。在单元格 $ (i, j) $ 中有一个数字 $ (i - 1) \cdot m + j $ ，即 $ a_{ij} = (i - 1) \cdot m + j $ 。 一只乌龟最初站在单元格 $ (1, 1) $ 中，它想来到单元格 $ (n, m) $ 。从单元格 $ (i, j) $ 它可以一步转到单元格 $ (i + 1, j) $ 或 $ (i, j + 1) $ 之一，如果它存在的话。路径是一系列单元格，其中对于序列中的每两个相邻单元格，满足以下条件：乌龟可以一步从第一个单元格到达第二个单元格。路径的成本是写入路径单元格中的数字的总和。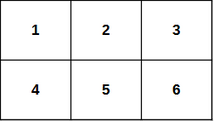 例如，$ n = 2 $ 和 $ m = 3 $ 表格将如上所示。海龟可以走以下路径： $ (1, 1) \rightarrow (1, 2) \rightarrow (1, 3) \rightarrow (2, 3) $ 。这种方式的成本等于 $ a_{11} + a_{12} + a_{13} + a_{23} = 12 $ 。另一方面，路径 $ (1, 1) \rightarrow (1, 2) \rightarrow (2, 2) \rightarrow (2, 1) $ 和 $ (1, 1) \rightarrow (1, 3) $是不正确的，因为在第一条路径中乌龟不能迈出一步 $ (2, 2) \rightarrow (2, 1) $ ，而在第二条路径中它不能迈出一步 $ (1, 1) \右箭头 (1, 3) $ 。 你被要求告诉海龟从单元 $ (1, 1) $ 到单元 $ (n, m) $ 的路径的最小可能成本。请注意，单元格 $ (1, 1) $ 和 $ (n, m) $ 是其中的一部分。

第一行包含一个整数 $ t $ ( $ 1 \leq t \leq 1000 $ ) — 测试用例的数量。测试用例的描述如下。 每个测试用例的一行包含两个整数 $ n $ 和 $ m $ ( $ 1 \leq n, m \leq 10^4 $ ) — 分别是表 $ a $ 的行数和列数。

对于每个测试用例，输出一个整数——从单元格 $ (1, 1) $ 到单元格 $ (n, m) $ 的路径的最小可能成本。 ## 样例#1 ### 样例输入示例 #1 ``` 7 1 1 2 3 3 2 7 1 1 10 5 5 10000 10000 ``` ### 样例输出#1 ``` 1 12 13 28 55 85 500099995000 ```

在第一个测试用例中，唯一可能的路径由单个单元格 $ (1, 1) $ 组成。 语句中显示了第二个测试用例中成本最低的路径。 在第四和第五个测试用例中，从 $ (1, 1) $ 到 $ (n, m) $ 只有一条路径。两条路径都访问表中的每个单元格。