CF1702G2 Passable Paths (hard version)
题目描述
这是该问题的困难版本。简单版本与困难版本的唯一区别在于查询的数量不同。
Polycarp 种下了一棵有 $n$ 个顶点的树。我们提醒你,$n$ 个顶点的树是一个无向连通图,包含 $n$ 个顶点和 $n-1$ 条边,且不包含环。
他称一个顶点集合是可通行的,如果存在一条树上的路径,能够经过该集合中的每一个顶点,且不会重复经过任何一条边。该路径可以经过集合外的其他顶点。
换句话说,如果存在一条简单路径,经过该集合中的所有顶点(也可以经过其他顶点),那么这个集合被称为可通行的。
例如,对于下图中的树,集合 $\{3, 2, 5\}$、$\{1, 5, 4\}$、$\{1, 4\}$ 是可通行的,而 $\{1, 3, 5\}$、$\{1, 2, 3, 4, 5\}$ 不是可通行的。
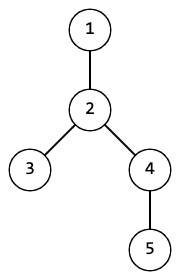
Polycarp 现在要你回答 $q$ 个查询。每个查询给出一个顶点集合,你需要判断该集合是否为可通行集合。
输入格式
输入的第一行包含一个整数 $n$($1 \le n \le 2 \cdot 10^5$),表示顶点数。
接下来的 $n-1$ 行描述树的结构。
每行包含两个整数 $u$ 和 $v$($1 \le u, v \le n$,$u \ne v$),表示一条连接顶点 $u$ 和 $v$ 的边。
接下来一行包含一个整数 $q$($1 \le q \le 10^5$),表示查询的数量。
接下来的 $2 \cdot q$ 行描述每个查询的集合。
每个集合的描述第一行为一个整数 $k$($1 \le k \le n$),表示集合的大小。
第二行为 $k$ 个互不相同的整数 $p_1, p_2, \dots, p_k$($1 \le p_i \le n$),表示集合中的顶点编号。
保证所有查询中 $k$ 的总和不超过 $2 \cdot 10^5$。
输出格式
输出 $q$ 行,每行对应一个查询的答案。如果集合是可通行的,输出 "YES",否则输出 "NO"。
答案不区分大小写(例如 "yEs"、"yes"、"Yes" 和 "YES" 都被认为是肯定答案)。
说明/提示
由 ChatGPT 4.1 翻译