CF1703E Mirror Grid
Description
You are given a square grid with $ n $ rows and $ n $ columns. Each cell contains either $ 0 $ or $ 1 $ .
In an operation, you can select a cell of the grid and flip it (from $ 0 \to 1 $ or $ 1 \to 0 $ ). Find the minimum number of operations you need to obtain a square that remains the same when rotated $ 0^{\circ} $ , $ 90^{\circ} $ , $ 180^{\circ} $ and $ 270^{\circ} $ .
The picture below shows an example of all rotations of a grid.
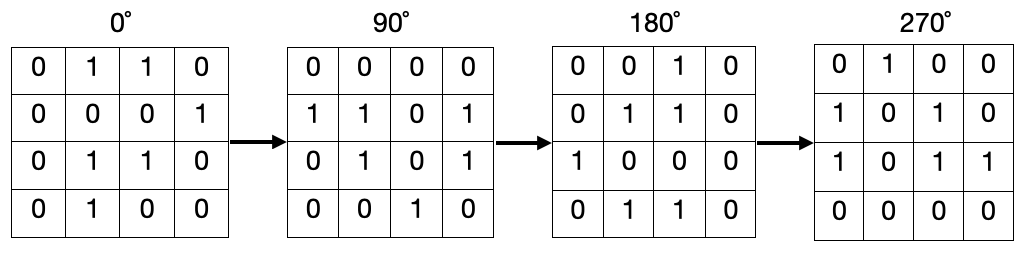
Input Format
The first line contains a single integer $ t $ ( $ 1 \leq t \leq 100 $ ) — the number of test cases.
The first line of each test case contains a single integer $ n $ ( $ 1 \leq n \leq 100 $ ) — the size of the grid.
Then $ n $ lines follow, each with $ n $ characters $ a_{i,j} $ ( $ 0 \leq a_{i,j} \leq 1 $ ) — the number written in each cell.
Output Format
For each test case output a single integer — the minimum number of operations needed to make the square look the same rotated $ 0^{\circ} $ , $ 90^{\circ} $ , $ 180^{\circ} $ and $ 270^{\circ} $ .
Explanation/Hint
In the first test case, we can perform one operations to make the grid $ \begin{matrix}0 & 1 & 0\\ 1 & 1 & \color{red}{1}\\ 0 & 1 & 0\end{matrix} $ . Now, all rotations of the square are the same.
In the second test case, all rotations of the square are already the same, so we don't need any flips.