CF1706B Making Towers

你有一个长度为 $n$ 的彩色方块序列。第 $i$ 个方块的颜色为 $c_i$，其中 $c_i$ 是 $1$ 到 $n$ 之间的整数。 你将按照如下方式依次将这些方块放置在无限大的坐标网格上： 1. 首先，将第 $1$ 个方块放在 $(0, 0)$。 2. 对于 $2 \le i \le n$，如果第 $i-1$ 个方块被放在 $(x, y)$，那么第 $i$ 个方块可以被放在 $(x+1, y)$、$(x-1, y)$ 或 $(x, y+1)$ 中的一个位置（但不能放在 $(x, y-1)$），且不能放在之前已经有方块的位置。 一座“塔”由 $s$ 个方块组成，这些方块被放在 $(x, y), (x, y+1), \ldots, (x, y+s-1)$ 这些位置上，其中 $(x, y)$ 是某个位置，$s$ 是整数。塔的大小为 $s$，即其中方块的数量。颜色为 $r$ 的塔指的是所有方块颜色均为 $r$ 的塔。 对于每种颜色 $r$（$1$ 到 $n$），请独立解决如下问题： - 按照上述规则放置方块，能形成的颜色为 $r$ 的塔的最大大小是多少？

第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 10^5$）。 每个测试用例的第二行包含 $n$ 个整数 $c_1, c_2, \ldots, c_n$（$1 \le c_i \le n$）。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出 $n$ 个整数。第 $r$ 个数表示按照题目规则能形成的颜色为 $r$ 的塔的最大大小。如果无法形成颜色为 $r$ 的塔，则输出 $0$。

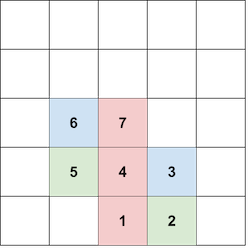
在第一个测试用例中，形成一个颜色为 $1$ 且大小为 $3$ 的塔的一种可能方式如下： - 将第 $1$ 个方块放在 $(0, 0)$； - 将第 $2$ 个方块放在第 $1$ 个方块的右侧，即 $(1, 0)$； - 将第 $3$ 个方块放在第 $2$ 个方块的上方，即 $(1, 1)$； - 将第 $4$ 个方块放在第 $3$ 个方块的左侧，即 $(0, 1)$； - 将第 $5$ 个方块放在第 $4$ 个方块的左侧，即 $(-1, 1)$； - 将第 $6$ 个方块放在第 $5$ 个方块的上方，即 $(-1, 2)$； - 将第 $7$ 个方块放在第 $6$ 个方块的右侧，即 $(0, 2)$。  位于 $(0, 0)$、$(0, 1)$ 和 $(0, 2)$ 的方块颜色均为 $1$，它们组成了一个大小为 $3$ 的塔。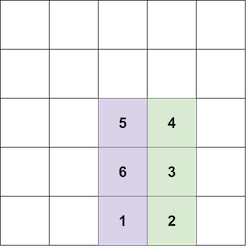 在第二个测试用例中，注意如下放置方式是不合法的，因为不允许将第 $6$ 个方块放在第 $5$ 个方块的下方：  可以证明无法形成颜色为 $4$ 且大小为 $3$ 的塔。 由 ChatGPT 4.1 翻译