CF1706B Making Towers

You have a sequence of $ n $ colored blocks. The color of the $ i $ -th block is $ c_i $ , an integer between $ 1 $ and $ n $ . You will place the blocks down in sequence on an infinite coordinate grid in the following way. 1. Initially, you place block $ 1 $ at $ (0, 0) $ . 2. For $ 2 \le i \le n $ , if the $ (i - 1) $ -th block is placed at position $ (x, y) $ , then the $ i $ -th block can be placed at one of positions $ (x + 1, y) $ , $ (x - 1, y) $ , $ (x, y + 1) $ (but not at position $ (x, y - 1) $ ), as long no previous block was placed at that position. A tower is formed by $ s $ blocks such that they are placed at positions $ (x, y), (x, y + 1), \ldots, (x, y + s - 1) $ for some position $ (x, y) $ and integer $ s $ . The size of the tower is $ s $ , the number of blocks in it. A tower of color $ r $ is a tower such that all blocks in it have the color $ r $ . For each color $ r $ from $ 1 $ to $ n $ , solve the following problem independently: - Find the maximum size of a tower of color $ r $ that you can form by placing down the blocks according to the rules.

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 10^5 $ ). The second line of each test case contains $ n $ integers $ c_1, c_2, \ldots, c_n $ ( $ 1 \le c_i \le n $ ). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output $ n $ integers. The $ r $ -th of them should be the maximum size of an tower of color $ r $ you can form by following the given rules. If you cannot form any tower of color $ r $ , the $ r $ -th integer should be $ 0 $ .

In the first test case, one of the possible ways to form a tower of color $ 1 $ and size $ 3 $ is: - place block $ 1 $ at position $ (0, 0) $ ; - place block $ 2 $ to the right of block $ 1 $ , at position $ (1, 0) $ ; - place block $ 3 $ above block $ 2 $ , at position $ (1, 1) $ ; - place block $ 4 $ to the left of block $ 3 $ , at position $ (0, 1) $ ; - place block $ 5 $ to the left of block $ 4 $ , at position $ (-1, 1) $ ; - place block $ 6 $ above block $ 5 $ , at position $ (-1, 2) $ ; - place block $ 7 $ to the right of block $ 6 $ , at position $ (0, 2) $ . 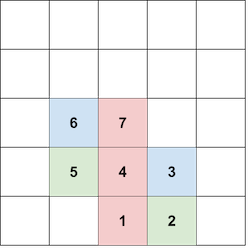The blocks at positions $ (0, 0) $ , $ (0, 1) $ , and $ (0, 2) $ all have color $ 1 $ , forming an tower of size $ 3 $ . 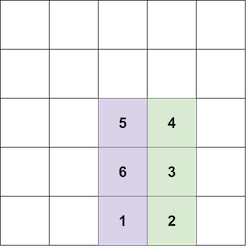In the second test case, note that the following placement is not valid, since you are not allowed to place block $ 6 $ under block $ 5 $ : It can be shown that it is impossible to form a tower of color $ 4 $ and size $ 3 $ .