CF1707C DFS Trees
题目描述
给定一个包含 $n$ 个顶点和 $m$ 条边的连通无向图。第 $i$ 条边的权值为 $i$。
下面是一个错误的寻找[最小生成树](https://en.wikipedia.org/wiki/Minimum_spanning_tree)(MST)的算法:
```
vis := 长度为 n 的数组
s := 边的集合
function dfs(u):
vis[u] := true
按边权从小到大遍历每一条与 u 相连的边 (u, v)
if vis[v] = false
将边 (u, v) 加入集合 s
dfs(v)
function findMST(u):
将 vis 数组全部重置为 false
将边集 s 重置为空
dfs(u)
返回边集 s
```
分别调用 findMST(1), findMST(2), ..., findMST(n) 时,每次都会得到一棵图的生成树。请判断这些生成树中哪些是最小生成树。
输入格式
第一行包含两个整数 $n$ 和 $m$($2\le n\le 10^5$,$n-1\le m\le 2\cdot 10^5$),表示图的顶点数和边数。
接下来的 $m$ 行,每行包含两个整数 $u_i$ 和 $v_i$($1\le u_i, v_i\le n$,$u_i\ne v_i$),表示一条无向边 $(u_i, v_i)$。输入中的第 $i$ 条边权值为 $i$。
保证图是连通的,且任意一对顶点之间至多有一条边。
输出格式
输出一个长度为 $n$ 的二进制字符串 $s$,其中 $s_i=1$ 表示 findMST(i) 得到的是最小生成树,$s_i=0$ 表示不是。
说明/提示
以下是第一个样例中给出的图。
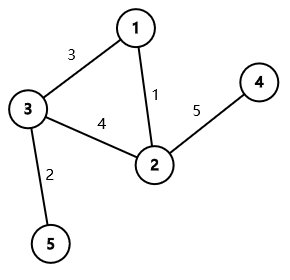
该图只有一棵最小生成树。最小生成树为 $(1,2),(3,5),(1,3),(2,4)$,总权值为 $1+2+3+5=11$。
下面是调用 findMST(1) 的部分过程:
- 重置 vis 数组和边集 s;
- 调用 dfs(1);
- vis[1] := true;
- 按权值从小到大遍历与 1 相连的边 $(1,2),(1,3)$;
- 将边 $(1,2)$ 加入边集 s,调用 dfs(2):
- vis[2] := true
- 按权值从小到大遍历与 2 相连的边 $(2,1),(2,3),(2,4)$;
- 因为 vis[1] = true,忽略边 $(2,1)$;
- 将边 $(2,3)$ 加入边集 s,调用 dfs(3):
- ...
最终选中的边为 $(1,2),(2,3),(3,5),(2,4)$,总权值为 $1+4+2+5=12>11$,因此 findMST(1) 得到的不是最小生成树。
可以证明,其他起点得到的生成树都是最小生成树,因此答案为 01111。
由 ChatGPT 4.1 翻译