CF1707C DFS Trees

You are given a connected undirected graph consisting of $ n $ vertices and $ m $ edges. The weight of the $ i $ -th edge is $ i $ . Here is a wrong algorithm of finding a [minimum spanning tree](https://en.wikipedia.org/wiki/Minimum_spanning_tree) (MST) of a graph: ``` vis := an array of length n s := a set of edges function dfs(u): vis[u] := true iterate through each edge (u, v) in the order from smallest to largest edge weight if vis[v] = false add edge (u, v) into the set (s) dfs(v) function findMST(u): reset all elements of (vis) to false reset the edge set (s) to empty dfs(u) return the edge set (s) ``` Each of the calls findMST(1), findMST(2), ..., findMST(n) gives you a spanning tree of the graph. Determine which of these trees are minimum spanning trees.

The first line of the input contains two integers $ n $ , $ m $ ( $ 2\le n\le 10^5 $ , $ n-1\le m\le 2\cdot 10^5 $ ) — the number of vertices and the number of edges in the graph. Each of the following $ m $ lines contains two integers $ u_i $ and $ v_i $ ( $ 1\le u_i, v_i\le n $ , $ u_i\ne v_i $ ), describing an undirected edge $ (u_i,v_i) $ in the graph. The $ i $ -th edge in the input has weight $ i $ . It is guaranteed that the graph is connected and there is at most one edge between any pair of vertices.

You need to output a binary string $ s $ , where $ s_i=1 $ if findMST(i) creates an MST, and $ s_i = 0 $ otherwise.

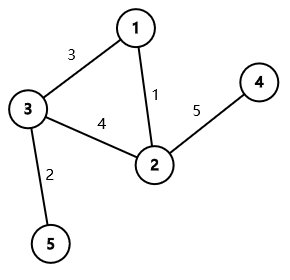Here is the graph given in the first example. There is only one minimum spanning tree in this graph. A minimum spanning tree is $ (1,2),(3,5),(1,3),(2,4) $ which has weight $ 1+2+3+5=11 $ . Here is a part of the process of calling findMST(1): - reset the array vis and the edge set s; - calling dfs(1); - vis\[1\] := true; - iterate through each edge $ (1,2),(1,3) $ ; - add edge $ (1,2) $ into the edge set s, calling dfs(2): - vis\[2\] := true - iterate through each edge $ (2,1),(2,3),(2,4) $ ; - because vis\[1\] = true, ignore the edge $ (2,1) $ ; - add edge $ (2,3) $ into the edge set s, calling dfs(3): - ... In the end, it will select edges $ (1,2),(2,3),(3,5),(2,4) $ with total weight $ 1+4+2+5=12>11 $ , so findMST(1) does not find a minimum spanning tree. It can be shown that the other trees are all MSTs, so the answer is 01111.