CF1710A Color the Picture

一幅画可以表示为一个 $n \times m$ 的网格（$n$ 行 $m$ 列），其中每个 $n \cdot m$ 个格子都被涂上了一种颜色。你有 $k$ 种不同颜色的颜料。每种颜料的数量有限，具体来说，第 $i$ 种颜料最多可以涂 $a_i$ 个格子。 如果每个格子至少有 $3$ 个与自身颜色相同的环面邻居，则这幅画被认为是美丽的。 如果两个格子在环面上共享一条边，则它们被认为是环面邻居。换句话说，对于某些整数 $1 \leq x_1, x_2 \leq n$ 和 $1 \leq y_1, y_2 \leq m$，如果下列两个条件之一成立，则第 $x_1$ 行第 $y_1$ 列的格子是第 $x_2$ 行第 $y_2$ 列的格子的环面邻居： - $x_1 - x_2 \equiv \pm1 \pmod{n}$ 且 $y_1 = y_2$，或者 - $y_1 - y_2 \equiv \pm1 \pmod{m}$ 且 $x_1 = x_2$。 注意，每个格子恰好有 $4$ 个环面邻居。例如，如果 $n=3$ 且 $m=4$，则格子 $(1, 2)$（第一行第二列）的环面邻居为：$(3, 2)$、$(2, 2)$、$(1, 3)$、$(1, 1)$。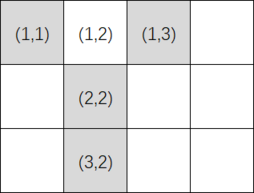如下图所示，灰色格子为 $(1, 2)$ 的环面邻居：  请判断，是否可以用给定的颜料将所有格子涂色，并且使得这幅画是美丽的？

每组测试数据包含多个测试用例。第一行包含测试用例数量 $t$（$1 \leq t \leq 10^4$）。接下来是每个测试用例的描述。 每个测试用例的第一行包含三个整数 $n$、$m$ 和 $k$（$3 \leq n, m \leq 10^9$，$1 \leq k \leq 10^5$），分别表示画的行数、列数和颜料种类数。 下一行包含 $k$ 个整数 $a_1, a_2, \dots, a_k$（$1 \leq a_i \leq 10^9$），其中 $a_i$ 表示第 $i$ 种颜料最多可以涂色的格子数。 保证所有测试用例中 $k$ 的总和不超过 $10^5$。

对于每个测试用例，如果可以涂出一幅美丽的画，输出 "Yes"（不带引号）；否则输出 "No"（不带引号）。

在第一个测试用例中，一种可能的涂色方案如下：  在第三个测试用例中，可以用颜料 $1$ 涂满所有格子。 由 ChatGPT 4.1 翻译