CF1710B Rain

你拥有一块可以被建模为无限直线的收割田地，其位置由整数标识。 接下来的 $n$ 天都会下雨。在第 $i$ 天，雨水将以位置 $x_i$ 为中心，强度为 $p_i$。由于这些降雨，某些位置会积累雨量；设 $a_j$ 表示整数位置 $j$ 处累计的雨量。初始时 $a_j$ 为 $0$，在第 $i$ 天降雨后，$a_j$ 会增加 $\max(0, p_i - |x_i - j|)$。 如果在任意时刻，存在某个位置 $j$ 满足累计雨量 $a_j > m$，你的田地就会被洪水淹没。 你可以使用一个魔法，将某一天的降雨完全抹去，即将 $p_i$ 设为 $0$。对于每个 $i$（$1 \leq i \leq n$），判断如果抹去第 $i$ 天的降雨，是否可以避免洪水发生。

每个测试包含多组测试用例。第一行包含测试用例数 $t$（$1 \leq t \leq 10^4$）。接下来是每组测试用例的描述。 每组测试用例的第一行包含两个整数 $n$ 和 $m$（$1 \leq n \leq 2 \cdot 10^5$，$1 \leq m \leq 10^9$），分别表示下雨天数和不会发生洪水的最大累计雨量。 接下来 $n$ 行，每行包含两个整数 $x_i$ 和 $p_i$（$1 \leq x_i, p_i \leq 10^9$），分别表示第 $i$ 天降雨的位置和强度。 所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每组测试用例，输出一个长度为 $n$ 的二进制字符串 $s$。如果抹去第 $i$ 天的降雨后不会发生洪水，则 $s$ 的第 $i$ 个字符为 $1$；否则为 $0$。

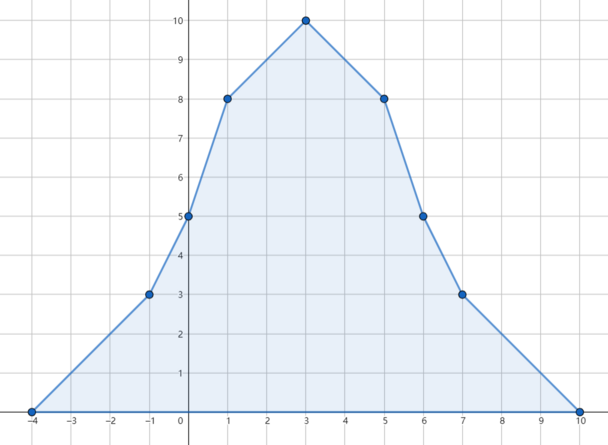
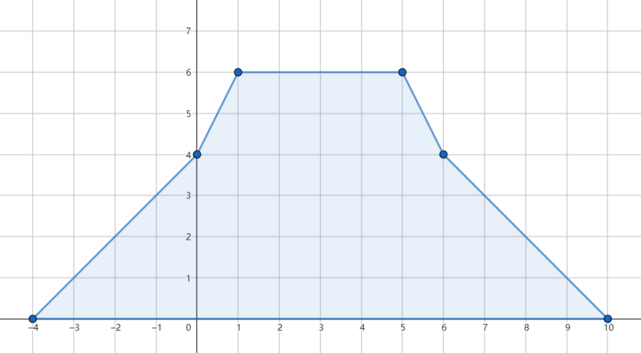
在第一个测试用例中，如果不使用魔法，累计雨量分布如下图所示：  如果抹去第三天的降雨，可以避免洪水，累计雨量分布如下：  在第二个测试用例中，最初就不会发生洪水，因此可以抹去任意一天的降雨。 在第三个测试用例中，无论如何都无法避免洪水。 由 ChatGPT 4.1 翻译