CF1710B Rain

You are the owner of a harvesting field which can be modeled as an infinite line, whose positions are identified by integers. It will rain for the next $ n $ days. On the $ i $ -th day, the rain will be centered at position $ x_i $ and it will have intensity $ p_i $ . Due to these rains, some rainfall will accumulate; let $ a_j $ be the amount of rainfall accumulated at integer position $ j $ . Initially $ a_j $ is $ 0 $ , and it will increase by $ \max(0,p_i-|x_i-j|) $ after the $ i $ -th day's rain. A flood will hit your field if, at any moment, there is a position $ j $ with accumulated rainfall $ a_j>m $ . You can use a magical spell to erase exactly one day's rain, i.e., setting $ p_i=0 $ . For each $ i $ from $ 1 $ to $ n $ , check whether in case of erasing the $ i $ -th day's rain there is no flood.

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \leq t \leq 10^4 $ ). The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ m $ ( $ 1 \leq n \leq 2 \cdot 10^5 $ , $ 1 \leq m \leq 10^9 $ ) — the number of rainy days and the maximal accumulated rainfall with no flood occurring. Then $ n $ lines follow. The $ i $ -th of these lines contains two integers $ x_i $ and $ p_i $ ( $ 1 \leq x_i,p_i \leq 10^9 $ ) — the position and intensity of the $ i $ -th day's rain. The sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output a binary string $ s $ length of $ n $ . The $ i $ -th character of $ s $ is 1 if after erasing the $ i $ -th day's rain there is no flood, while it is 0, if after erasing the $ i $ -th day's rain the flood still happens.

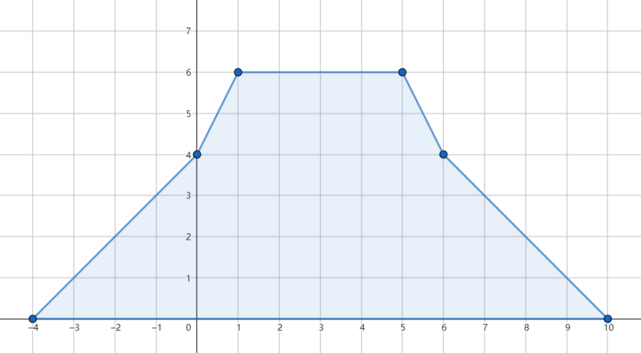
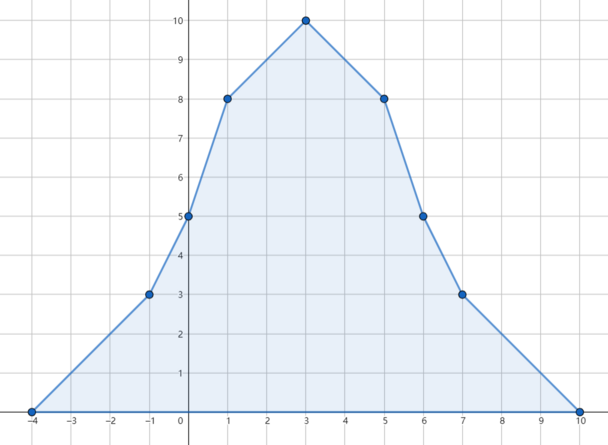In the first test case, if we do not use the spell, the accumulated rainfall distribution will be like this: If we erase the third day's rain, the flood is avoided and the accumulated rainfall distribution looks like this: In the second test case, since initially the flood will not happen, we can erase any day's rain. In the third test case, there is no way to avoid the flood.