CF1712D Empty Graph

— Do you have a wish? — I want people to stop gifting each other arrays. O_o and Another Young Boy An array of $ n $ positive integers $ a_1,a_2,\ldots,a_n $ fell down on you from the skies, along with a positive integer $ k \le n $ . You can apply the following operation at most $ k $ times: - Choose an index $ 1 \le i \le n $ and an integer $ 1 \le x \le 10^9 $ . Then do $ a_i := x $ (assign $ x $ to $ a_i $ ). Then build a [complete](https://en.wikipedia.org/wiki/Complete_graph) undirected weighted graph with $ n $ vertices numbered with integers from $ 1 $ to $ n $ , where edge $ (l, r) $ ( $ 1 \le l < r \le n $ ) has weight $ \min(a_{l},a_{l+1},\ldots,a_{r}) $ . You have to find the maximum possible diameter of the resulting graph after performing at most $ k $ operations. The diameter of a graph is equal to $ \max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)} $ , where $ \operatorname{d}(u, v) $ is the length of the shortest path between vertex $ u $ and vertex $ v $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). Description of the test cases follows. The first line of each test case contains two integers $ n $ and $ k $ ( $ 2 \le n \le 10^5 $ , $ 1 \le k \le n $ ). The second line of each test case contains $ n $ positive integers $ a_1,a_2,\ldots,a_n $ ( $ 1 \le a_i \le 10^9 $ ). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .

For each test case print one integer — the maximum possible diameter of the graph after performing at most $ k $ operations.

In the first test case, one of the optimal arrays is $ [2,4,5] $ . The graph built on this array: 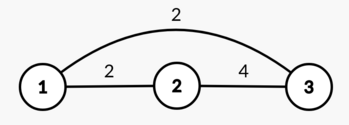 $ \operatorname{d}(1, 2) = \operatorname{d}(1, 3) = 2 $ and $ \operatorname{d}(2, 3) = 4 $ , so the diameter is equal to $ \max(2,2,4) = 4 $ .