CF1712F Triameter

— What is my mission? — To count graph diameters. You and Your Submission A tree is a connected undirected graph without cycles. A weighted tree has a weight assigned to each edge. The degree of a vertex is the number of edges connected to this vertex. You are given a weighted tree with $ n $ vertices, each edge has a weight of $ 1 $ . Let $ L $ be the set of vertices with degree equal to $ 1 $ . You have to answer $ q $ independent queries. In the $ i $ -th query: 1. You are given a positive integer $ x_i $ . 2. For all $ u,v \in L $ such that $ u < v $ , add edge $ (u, v) $ with weight $ x_i $ to the graph (initially the given tree). 3. Find the diameter of the resulting graph. The diameter of a graph is equal to $ \max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)} $ , where $ \operatorname{d}(u, v) $ is the length of the shortest path between vertex $ u $ and vertex $ v $ .

The first line contains a single integer $ n $ ( $ 3 \le n \le 10^6 $ ). The second line contains $ n - 1 $ integers $ p_2,p_3,\ldots,p_n $ ( $ 1 \le p_i < i $ ) indicating that there is an edge between vertices $ i $ and $ p_i $ . It is guaranteed that the given edges form a tree. The third line contains a single integer $ q $ ( $ 1 \le q \le 10 $ ). The fourth line contains $ q $ integers $ x_1,x_2,\ldots,x_q $ ( $ 1 \le x_i \le n $ ). All $ x_i $ are distinct.

Print $ q $ integers in a single line — the answers to the queries.

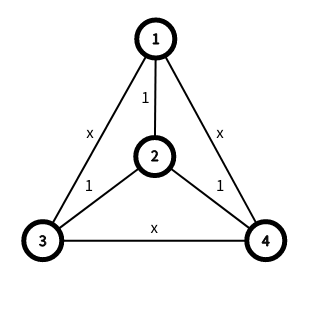
The graph in the first test after adding the edges: