CF1713A Traveling Salesman Problem

你正位于一个无限的笛卡尔坐标系的点 $ (x , y) $上，你可以进行四种操作： - 向左移动至 $ (x - 1, y) $ - 向右移动至 $ (x + 1, y) $ - 向上移动至 $ (x, y + 1) $ - 向下移动至 $ (x, y - 1) $ 有 $ n $ 个宝箱在这个平面上。 第 $ i $ 个 宝箱的坐标为 $ (x_i,y_i) $ . 保证每个宝箱都在 $ x $ 轴 或 $ y $ 轴上。即 $ x_i=0 $ 或 $ y_i=0 $。 你现在点 $ (0,0) $ 上，想将所有宝箱全部收入囊中，并回到原点。 你想知道你需要的最小移动次数是多少。 本题使用多组测试数据。

第一行包含一个整数 $ t $（$ 1 \le t \le 100 $）— 测试组数 对于每一组数据， 第一行包含一个整数 $ n $（$ 1 \le n \le 100 $）— 宝箱数量 第 $ i+1 $ 行 $ n $ 包含两个整数 $ x_i $ 和 $ y_i $（$ -100 \le x_i, y_i \le 100 $）— 第 $i$ 个宝箱的坐标，保证 $ x_i=0 $ 或 $ y_i=0 $。 注意每一组数据的 $n$ 的和是无限制的

共 $t$ 行，每行包含一个整数，即最小步数

In the first test case, a possible sequence of moves that uses the minimum number of moves required is shown below. 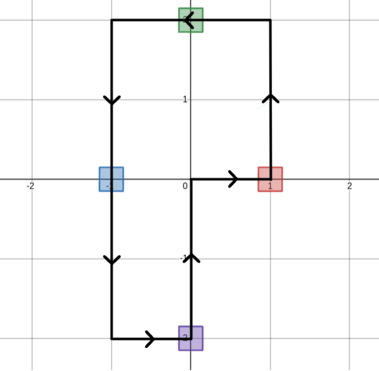 $ $$$(0,0) \to (1,0) \to (1,1) \to (1, 2) \to (0,2) \to (-1,2) \to (-1,1) \to (-1,0) \to (-1,-1) \to (-1,-2) \to (0,-2) \to (0,-1) \to (0,0) $ $

In the second test case, a possible sequence of moves that uses the minimum number of moves required is shown below.

$ $ (0,0) \to (0,1) \to (0,2) \to (-1, 2) \to (-2,2) \to (-3,2) \to (-3,1) \to (-3,0) \to (-3,-1) \to (-2,-1) \to (-1,-1) \to (0,-1) \to (0,0) $ $$$In the third test case, we can collect all boxes without making any moves.