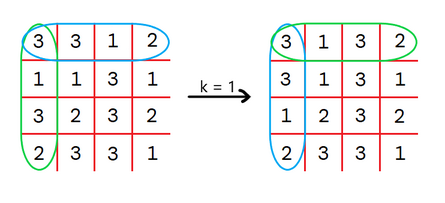
CF1713E Cross Swapping

You are given a square matrix $ A $ of size $ n \times n $ whose elements are integers. We will denote the element on the intersection of the $ i $ -th row and the $ j $ -th column as $ A_{i,j} $ . You can perform operations on the matrix. In each operation, you can choose an integer $ k $ , then for each index $ i $ ( $ 1 \leq i \leq n $ ), swap $ A_{i, k} $ with $ A_{k, i} $ . Note that cell $ A_{k, k} $ remains unchanged. 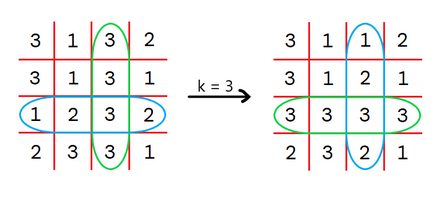For example, for $ n = 4 $ and $ k = 3 $ , this matrix will be transformed like this: The operation $ k = 3 $ swaps the blue row with the green column.You can perform this operation any number of times. Find the lexicographically smallest matrix $ ^\dagger $ you can obtain after performing arbitrary number of operations. $ {}^\dagger $ For two matrices $ A $ and $ B $ of size $ n \times n $ , let $ a_{(i-1) \cdot n + j} = A_{i,j} $ and $ b_{(i-1) \cdot n + j} = B_{i,j} $ . Then, the matrix $ A $ is lexicographically smaller than the matrix $ B $ when there exists an index $ i $ ( $ 1 \leq i \leq n^2 $ ) such that $ a_i < b_i $ and for all indices $ j $ such that $ 1 \leq j < i $ , $ a_j = b_j $ .

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 10^5 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 1 \leq n \leq 1000 $ ) — the size of the matrix. The $ i $ -th line of the next $ n $ lines contains $ n $ integers $ A_{i, 1}, A_{i, 2}, \dots, A_{i, n} $ ( $ 1 \le A_{i, j} \le 10^9 $ ) — description of the matrix $ A $ . It is guaranteed that the sum of $ n^2 $ over all test cases does not exceed $ 10^6 $ .

For each test case, print $ n $ lines with $ n $ integers each — the lexicographically smallest matrix.

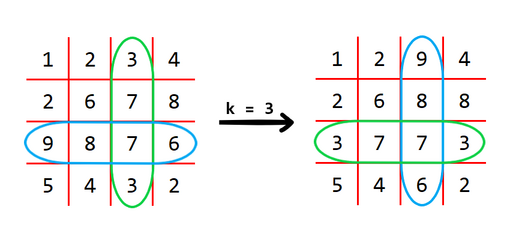
Note that in every picture below the matrix is transformed in such a way that the blue rows are swapped with the green columns. In the first test case, we can perform $ 1 $ operation for $ k = 3 $ . The matrix will be transformed as below: 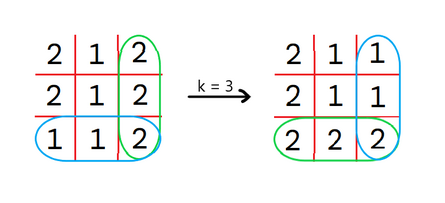 In the second test case, we can perform $ 2 $ operations for $ k = 1 $ and $ k = 3 $ :