CF1714G Path Prefixes

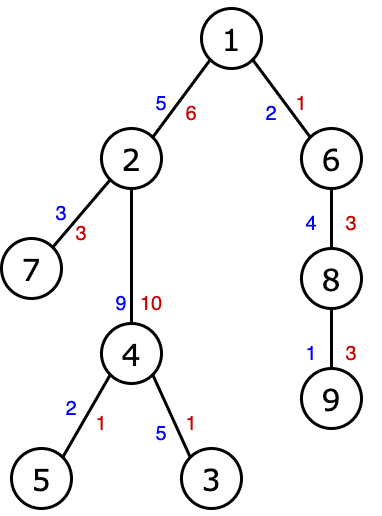
现有一颗以 $1$ 为根的树，节点编号从 $1$ 到 $n$。 每条边有两个权值，分别为 $a_j$ 和 $b_j$。 输出 $n-1$ 个数 $r_2,r_3\cdots,r_n$，其中 $r_i$ 定义如下： 考虑从根节点（$1$ 号节点）到第 $i$ 号节点 $(2\le i\le n)$ 的路径，令沿该路径每条边的花费 $a_j$ 之和为 $A_i$，则 $r_i$ 为该路径的最长前缀长度，使该前缀的 $b_j$ 之和不大于 $A_i$ .  以 $n=9$ 时为例，如上图，蓝色数字表示 $a_j$ 的花费，红色数字表示 $b_j$ 的花费。 在这种情况下： - $r_2=0$，因为到节点 $2$ 的路径中有 $a_j=5$，只有前缀为 $0$ 时才可能有较小（或相等）的 $b_j$； - $r_3=3$，因为到节点 $3$ 的路径中 $a_j$ 为 $5+9+5=19$，长为 $3$ 的前缀使 $b_j$ 为 $6+10+1=17(17\le19)$ 符合题意； - $r_4=1$，因为到节点 $4$ 的路径中 $a_j$ 为 $5+9=14$，长为 $1$ 的前缀使 $b_j$ 为 $6$（这是最长的符合题意的前缀，因为长为 $2$ 的前缀的 $b_j$ 为 $6+10=16$，大于 $ 14 $）； - $r_5=2$，因为到节点 $5$ 的路径中 $a_j$ 为 $5+9+2=16$，长为 $2$ 的前缀使 $b_j$ 为 $6+10=16$（是最长的符合题意的前缀，因为长为 $3$ 的前缀的 $b_j$ 为 $6+10+1=17$，比 $16$ 大）； - $r_6=1$，因为到节点 $6$ 的路径中 $a_j$ 为 $2$，长为 $1$ 的前缀使 $b_j$ 等于 $1$； - $r_7=1$，因为到节点 $7$ 的路径中 $a_j$ 为 $5+3=8$，长为 $1$ 的前缀使 $b_j$ 等于 $6$（这是最长的符合题意的前缀，因为长为 $2$ 的前缀的 $b_j$ 为 $6+3=9$，超出了期望的 $ 8 $）； - $r_8=2$，因为到节点 $8$ 的路径中 $a_j$ 为 $2+4=6$，长为 $2$ 的前缀使 $b_j$ 为 $1+3=4$； - $r_9=3$，因为到节点 $9$ 的路径中 $a_j$ 为 $2+4+1=7$，长为 $3$ 的前缀使 $b_j$ 为 $1+3+3=7$。

第一行有一个整数 $t(1\le t\le10^4)$ 表示测试组数。 每组样例以一个整数 $n(2\le n\le2\cdot10^5)$ 开始，表示这棵树的节点数。 接下来 $n-1$ 行，每行有三个整数 $p_j,a_j,b_j(1\le p_j\le n,1\le a_j,b_j\le10^9)$ 分别表示节点 $j$ 的祖先和从 $p_j$ 到 $j$ 的两个边权。 $j$ 的值从 $2$ 到 $n$。输入数据保证生成的是一颗以 $1$ 为根的树，且 $n$ 不超过 $2\cdot10^5$。

对于每一组输入，输出一行 $n-1$ 个数：$r_2,r_3,\dots,r_n$。

#### 样例解释 第一组样例解释在题目描述。 在第二组样例中： - $r_2=0$，因为到节点 $2$ 的路径中 $a_j$ 等于 $1$，只有前缀为 $0$ 时才可能有较小（或相等）的 $b_j$； - $r_3=0$，因为到节点 $3$ 的路径中 $a_j$ 为 $1+1=2$，长为 $1$ 的前缀使 $b_j$ 等于 $100( 100>2)$； - $r_4=3$，因为到节点 $4$ 的路径中 $a_j$ 为 $1+1+101=103$，长为 $3$ 的前缀使 $b_j$ 为 $102$。