CF1715A Crossmarket

Stanley 和 Megan 决定在“Crossmarket”杂货店购物，这家商店可以用一个 $n$ 行 $m$ 列的矩阵表示。 Stanley 和 Megan 每移动到一个相邻的格子需要消耗 $1$ 单位能量。如果两个格子有公共边，则它们被认为是相邻的。为了加快购物进程，Megan 带来了她的传送门，并且她每到一个格子（如果该格子还没有传送门）就会留下一个传送门。如果某个人（Stanley 或 Megan）在有传送门的格子上，他可以用 $1$ 单位能量传送到任意另一个有传送门的格子，包括 Megan 的起始格子。 他们决定分头行动：Stanley 将从左上角的格子（坐标为 $(1, 1)$）走到右下角的格子（坐标为 $(n, m)$），而 Megan 需要从左下角的格子（坐标为 $(n, 1)$）走到右上角的格子（坐标为 $(1, m)$）。 请问他们两人完成任务所需的最小总能量是多少？ 注意，他们可以自由选择移动的时机。时间不会影响能量消耗。

每个测试点包含多组测试数据。第一行包含测试用例数 $t$（$1 \le t \le 1000$）。接下来每组测试数据占一行，每行包含两个整数 $n$ 和 $m$（$1 \le n, m \le 10^5$）。

对于每组测试数据，输出一个整数，表示答案。

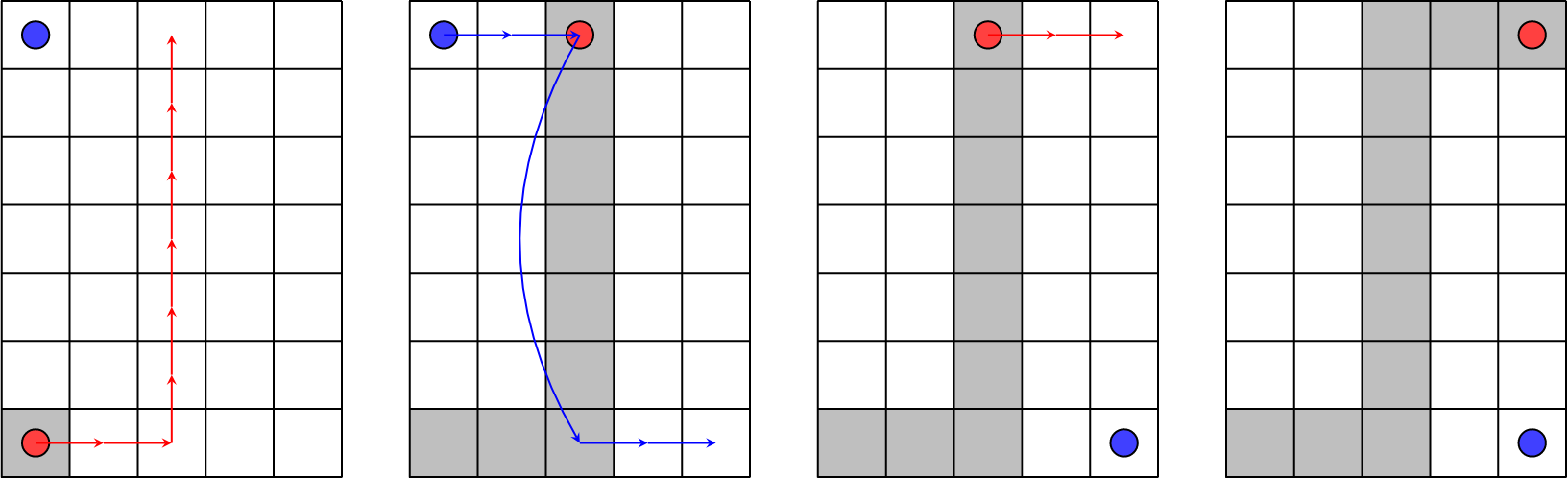
 在第一个测试用例中，他们可以按照以下方案行动： 1. Megan（红圈）移动到格子 $(7, 3)$，然后再前往格子 $(1, 3)$，Stanley（蓝圈）也做同样的操作。 2. Stanley 使用该格子的传送门（带有传送门的格子为灰色）传送到格子 $(7, 3)$，然后移动到他的终点——格子 $(7, 5)$。 3. Megan 也完成她的路线，前往格子 $(1, 5)$。 总能量消耗为 $(2+6)+(2+1+2)+(2)=15$，这就是最终答案。 由 ChatGPT 4.1 翻译