CF1717D Madoka and The Corruption Scheme

Madoka 决定负责组织一场大型电脑游戏锦标赛“OSU”！ 在本次锦标赛中，比赛采用“奥林匹克制”。也就是说，锦标赛共有 $2^n$ 名参赛者，编号为 $1$ 到 $2^n$ 的整数。锦标赛共进行 $n$ 轮。在第 $i$ 轮中，将有 $2^{n-i}$ 场比赛，每场比赛由两名选手（一名在左，一名在右）对决，胜者晋级下一轮，败者被淘汰。并且，下一轮中选手的相对顺序不会改变。最终，最后剩下的选手即为本次锦标赛的冠军。 但编号越小的选手，如果获胜，将会支付给 Madoka 更多的报酬，因此 Madoka 希望编号最小的选手能够获胜。为此，她可以自由安排第一轮的选手顺序，并且可以为每场比赛指定胜者（左侧或右侧选手）。 但是 Madoka 知道，锦标赛的赞助商最多可以更改 $k$ 场比赛的胜负结果。（也就是说，如果原本左侧选手获胜，被更改后则右侧选手获胜，反之亦然。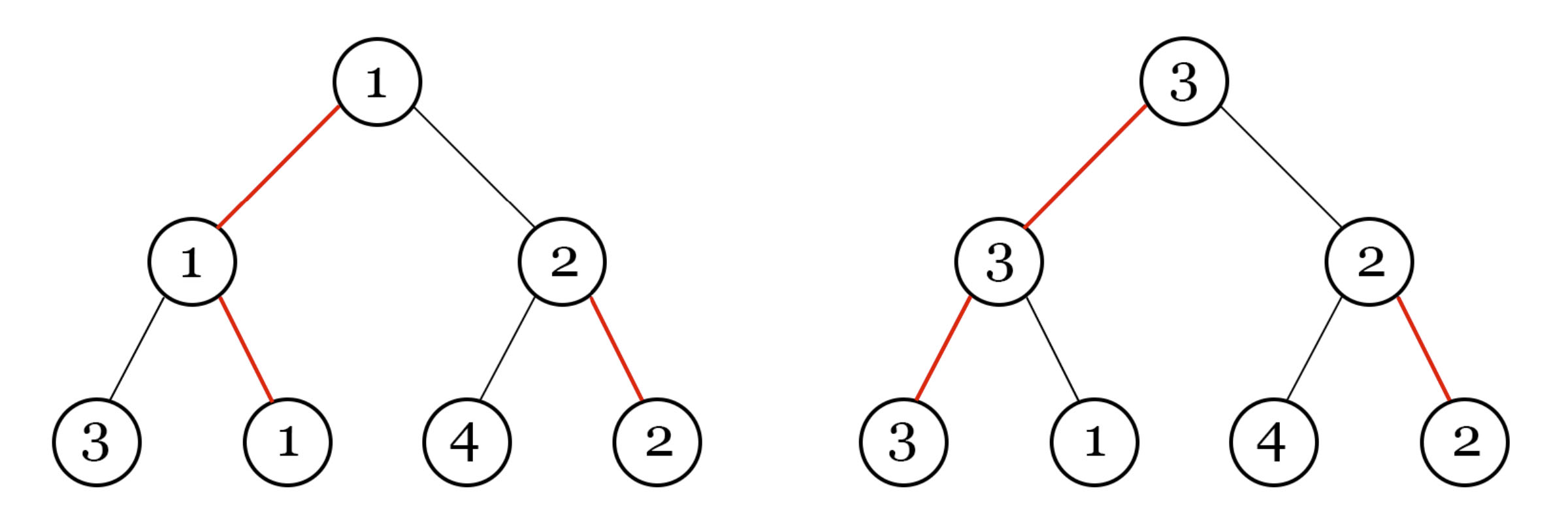）  上图左侧展示了 Madoka 安排的锦标赛对阵表，红线表示应当获胜的选手。右侧展示了赞助商更改了一场比赛结果（1号与3号选手的比赛）后的对阵表。 请输出无论赞助商如何更改比赛结果，Madoka 能够确保的冠军选手的最小编号。由于答案可能很大，请输出其对 $10^9+7$ 取模的结果。注意，需要先最小化答案，再取模。

输入仅一行，包含两个整数 $n$ 和 $k$（$1 \le n \le 10^5, 1 \le k \le \min(2^n - 1, 10^9)$），分别表示锦标赛的轮数和赞助商最多可以更改的比赛场数。

输出一个整数，表示 Madoka 能确保的冠军选手的最小编号，对 $10^9+7$ 取模。

在第一个样例中，只有一场比赛，1号和2号选手对决，因此赞助商总能让2号选手获胜。 第二个样例的对阵表如题面图片所示。 由 ChatGPT 4.1 翻译