CF1725C Circular Mirror

Pak Chanek has a mirror in the shape of a circle. There are $ N $ lamps on the circumference numbered from $ 1 $ to $ N $ in clockwise order. The length of the arc from lamp $ i $ to lamp $ i+1 $ is $ D_i $ for $ 1 \leq i \leq N-1 $ . Meanwhile, the length of the arc between lamp $ N $ and lamp $ 1 $ is $ D_N $ . Pak Chanek wants to colour the lamps with $ M $ different colours. Each lamp can be coloured with one of the $ M $ colours. However, there cannot be three different lamps such that the colours of the three lamps are the same and the triangle made by considering the three lamps as vertices is a right triangle (triangle with one of its angles being exactly $ 90 $ degrees). The following are examples of lamp colouring configurations on the circular mirror. 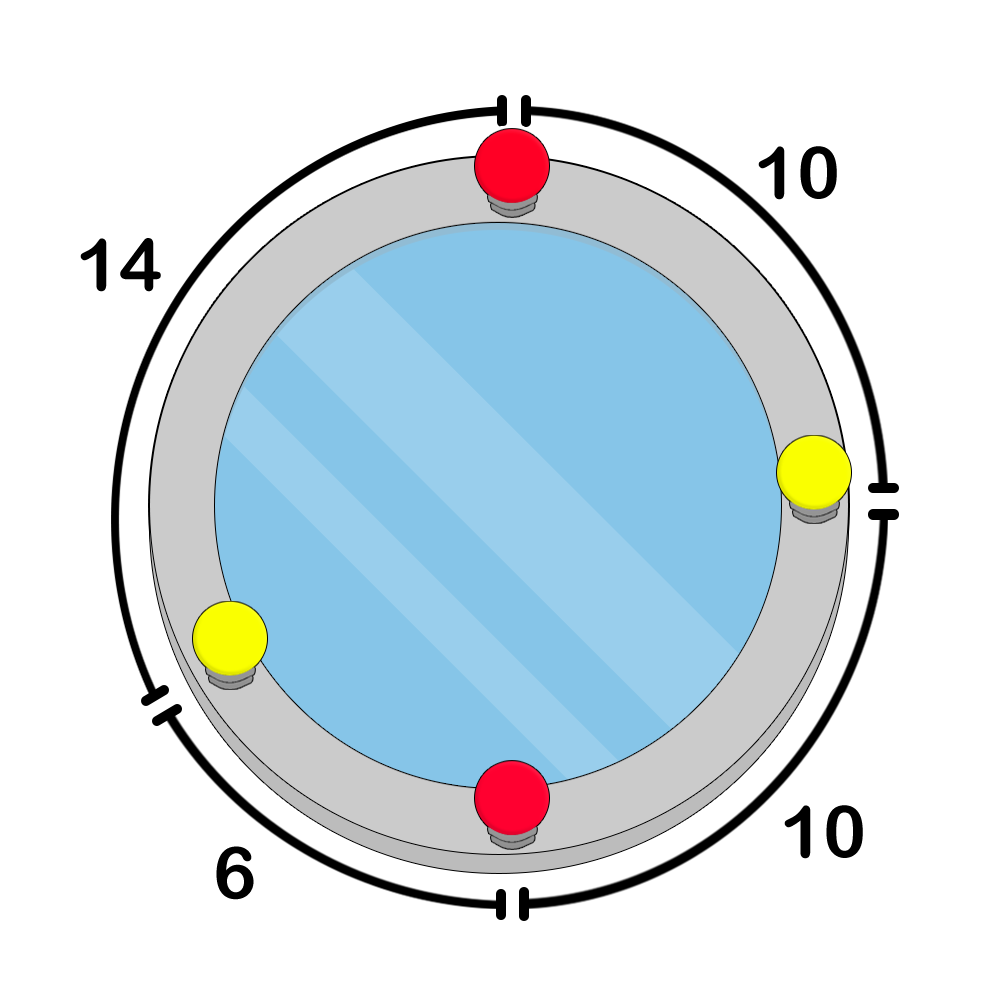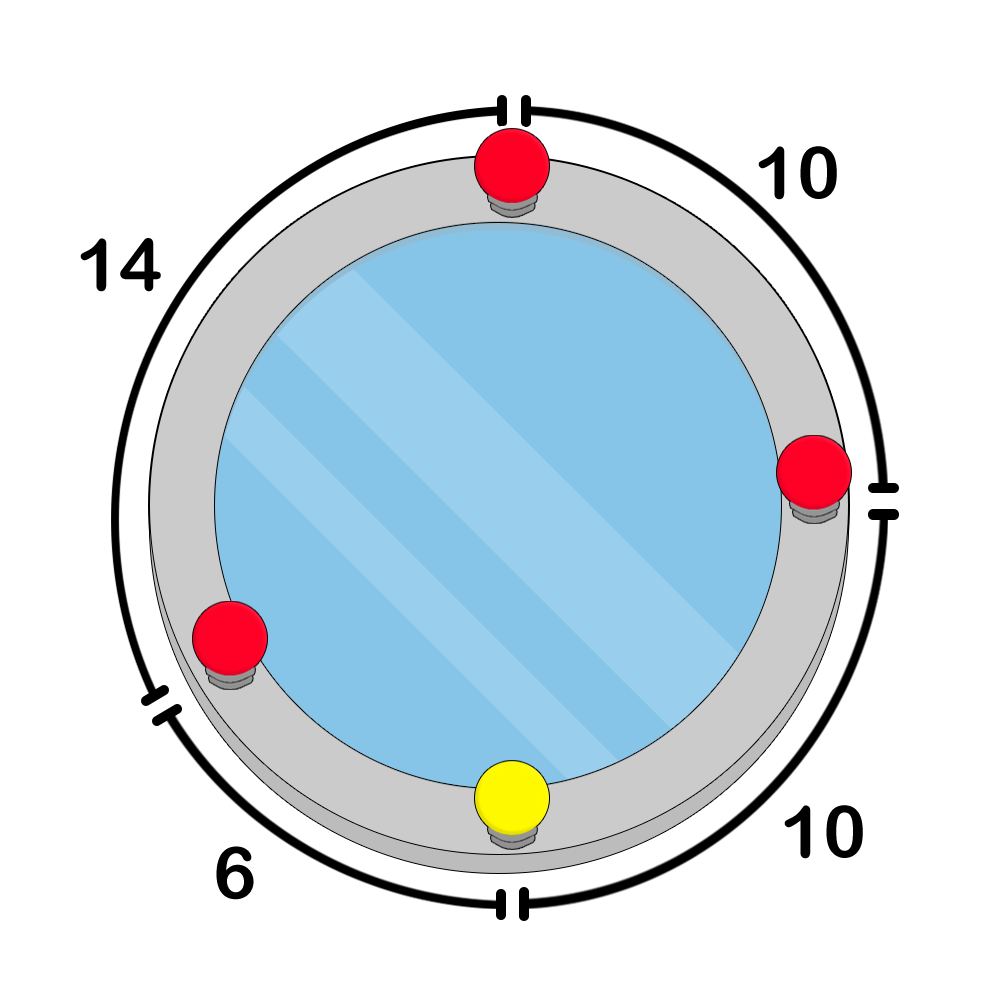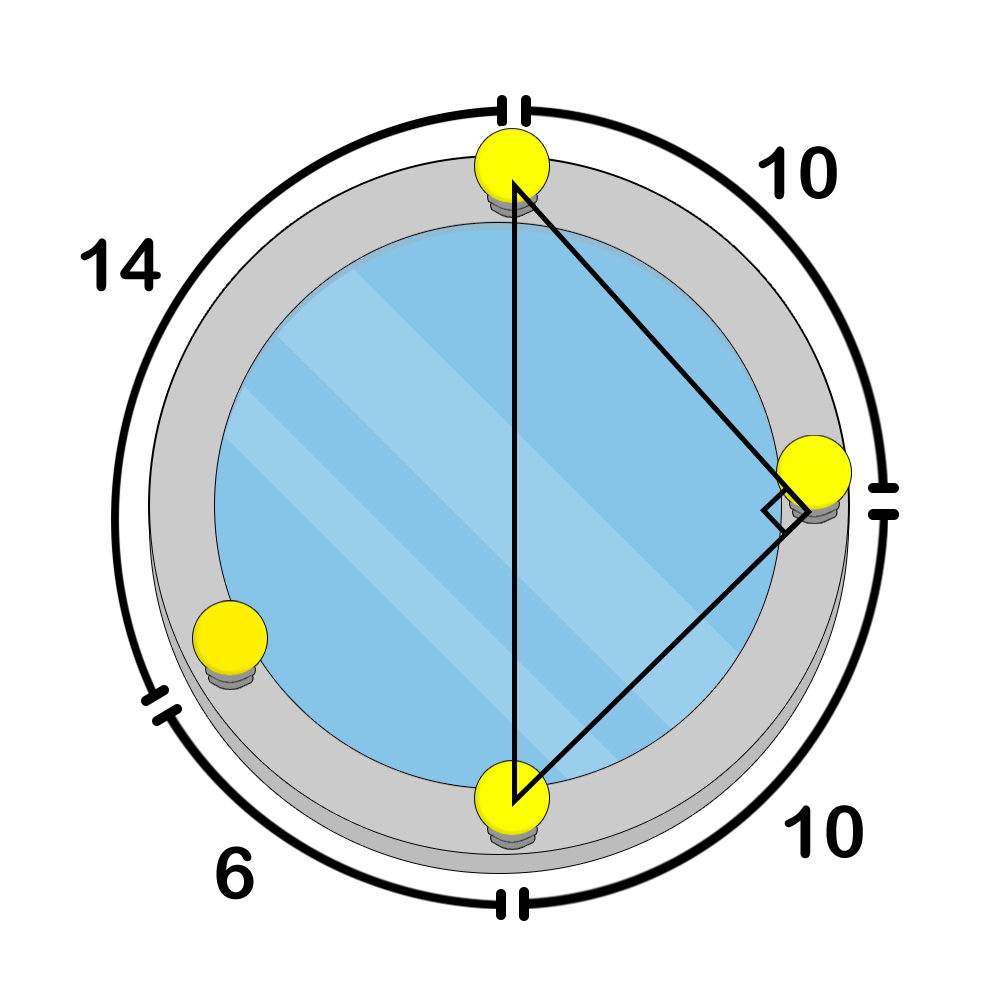Figure 1. an example of an incorrect colouring because lamps $ 1 $ , $ 2 $ , and $ 3 $ form a right triangleFigure 2. an example of a correct colouringFigure 3. an example of a correct colouringBefore colouring the lamps, Pak Chanek wants to know the number of distinct colouring configurations he can make. Count the number of distinct possible lamp colouring configurations, modulo $ 998\,244\,353 $ .

The first line contains two integers $ N $ and $ M $ ( $ 1 \le N \le 3 \cdot 10^5 $ , $ 2 \le M \le 3 \cdot 10^5 $ ) — the number of lamps in the mirror and the number of different colours used. The second line contains $ N $ integers $ D_1, D_2, \ldots, D_N $ ( $ 1 \le D_i \le 10^9 $ ) — the lengths of the arcs between the lamps in the mirror.

An integer representing the number of possible lamp colouring configurations, modulo $ 998\,244\,353 $ .

In the first example, all correct lamp colouring configurations are $ [1, 1, 2, 1] $ , $ [1, 1, 2, 2] $ , $ [1, 2, 1, 2] $ , $ [1, 2, 2, 1] $ , $ [1, 2, 2, 2] $ , $ [2, 1, 1, 1] $ , $ [2, 1, 1, 2] $ , $ [2, 1, 2, 1] $ , $ [2, 2, 1, 1] $ , and $ [2, 2, 1, 2] $ .