CF1725C Circular Mirror

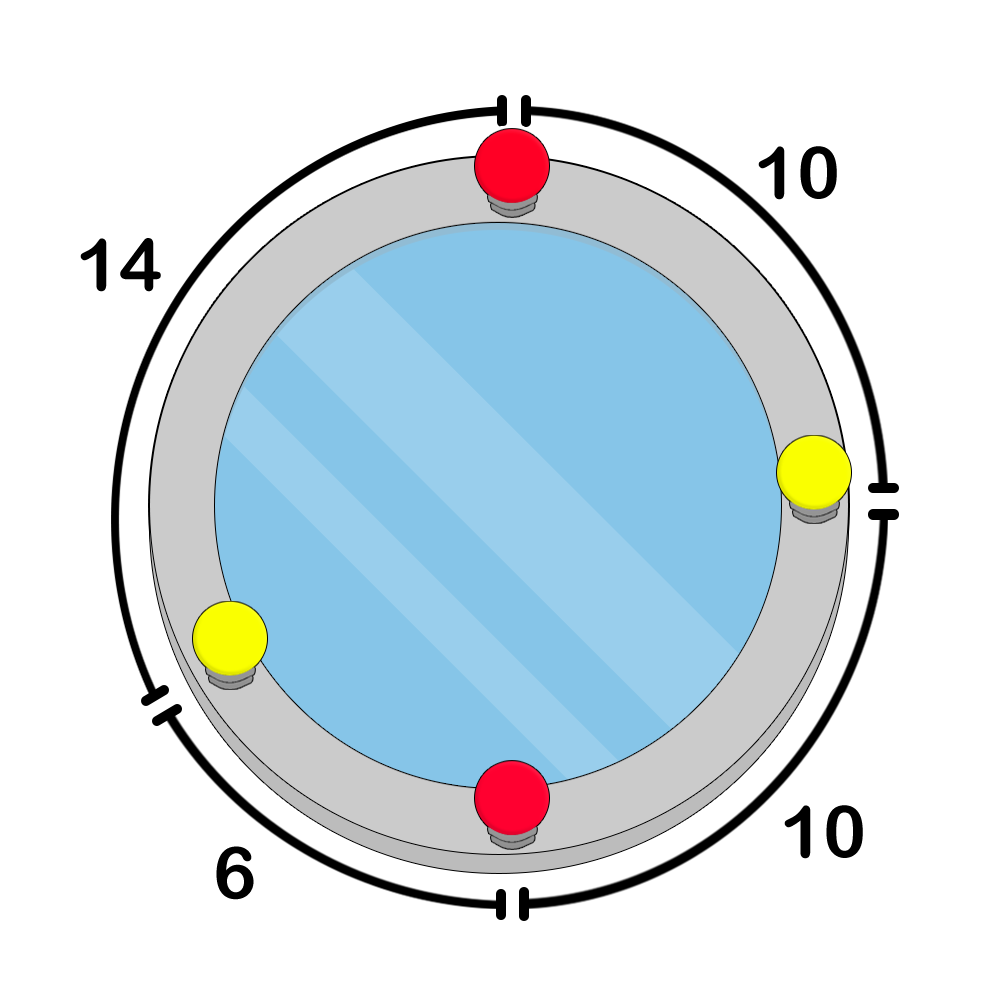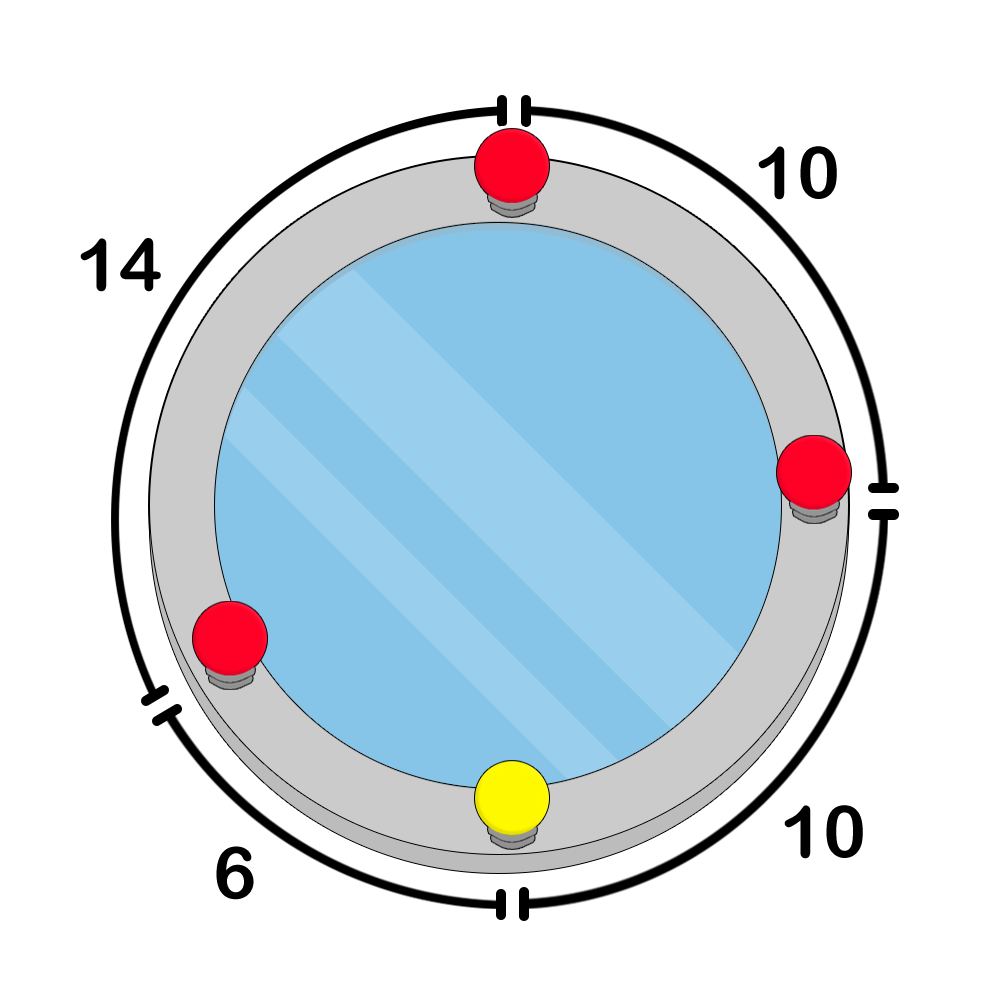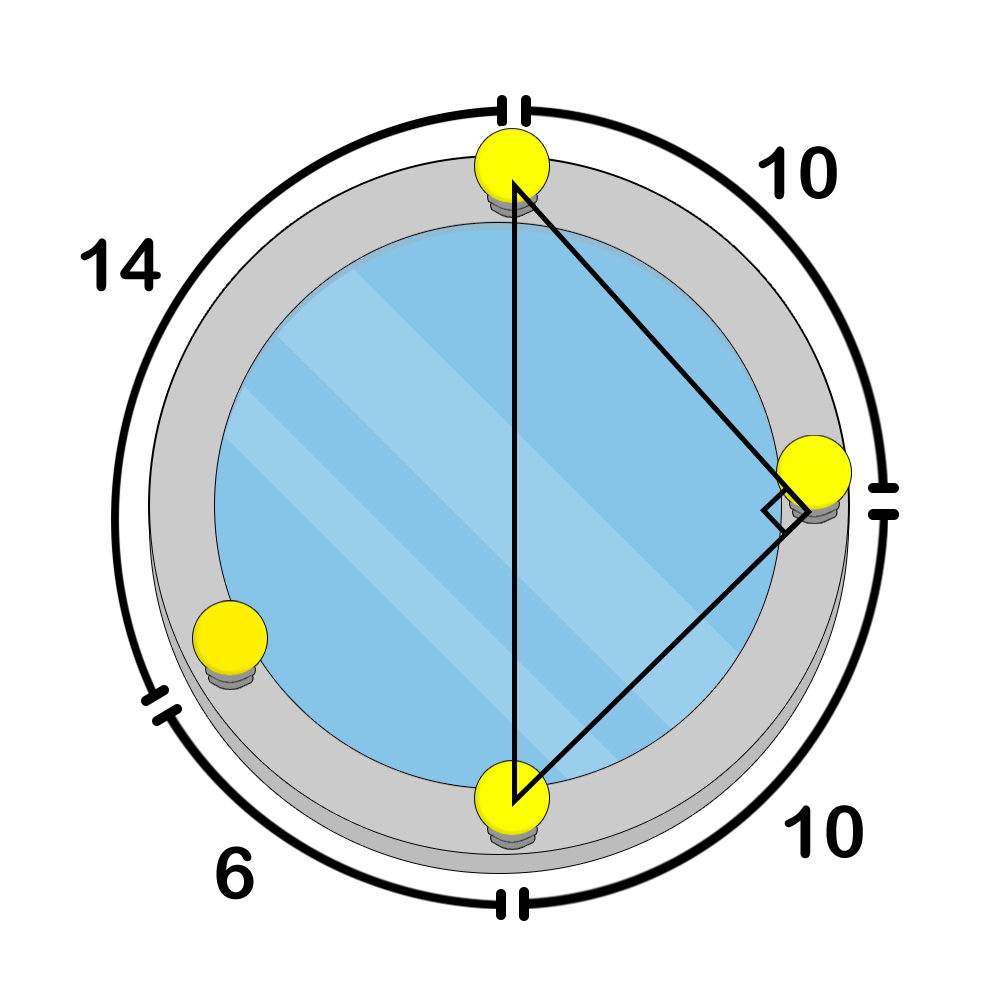
Pak Chanek 有一面圆形的镜子。镜子的圆周上有 $N$ 盏灯，顺时针编号为 $1$ 到 $N$。从第 $i$ 盏灯到第 $i+1$ 盏灯的弧长为 $D_i$，其中 $1 \leq i \leq N-1$。而第 $N$ 盏灯到第 $1$ 盏灯之间的弧长为 $D_N$。 Pak Chanek 想用 $M$ 种不同的颜色给这些灯染色。每盏灯可以被染成 $M$ 种颜色中的一种。但是，不允许存在三盏不同的灯，使得这三盏灯的颜色相同，并且以这三盏灯为顶点所构成的三角形是直角三角形（即其中一个角恰好为 $90$ 度）。 以下是圆镜上灯的染色配置示例。  图 1：一个错误的染色示例，因为第 $1$、$2$、$3$ 盏灯构成了一个直角三角形。 图 2：一个正确的染色示例。 图 3：一个正确的染色示例。 在给灯染色之前，Pak Chanek 想知道他可以进行多少种不同的合法染色方案。请计算不同的合法灯染色方案数，答案对 $998\,244\,353$ 取模。

第一行包含两个整数 $N$ 和 $M$（$1 \leq N \leq 3 \cdot 10^5$，$2 \leq M \leq 3 \cdot 10^5$），分别表示镜子上的灯数和可用的不同颜色数。 第二行包含 $N$ 个整数 $D_1, D_2, \ldots, D_N$（$1 \leq D_i \leq 10^9$），表示镜子上相邻两盏灯之间的弧长。

输出一个整数，表示可能的合法灯染色方案数，对 $998\,244\,353$ 取模。

在第一个样例中，所有合法的灯染色方案为 $[1, 1, 2, 1]$、$[1, 1, 2, 2]$、$[1, 2, 1, 2]$、$[1, 2, 2, 1]$、$[1, 2, 2, 2]$、$[2, 1, 1, 1]$、$[2, 1, 1, 2]$、$[2, 1, 2, 1]$、$[2, 2, 1, 1]$ 和 $[2, 2, 1, 2]$。 由 ChatGPT 4.1 翻译