CF1725F Field Photography

PC 正在前往马纳多。原来，2019年印度尼西亚国家科学奥林匹克运动会正在举行。OSN 2019的参赛者目前正在一个待拍照的场地排队。该场地的形状类似于一个大小为 $N\times 10^{100}$ 的网格，有$N$行和$10^{100}$列。行从北到南从 $1$ 编号到 $N$ ，列从西到东从 $1$ 编号到 $10^{100}$ 。第 $r$ 行第 $c$ 列的方格坐标为$(r,c)$。 有 $N$ 个省份参加 OSN 2019。最初，代表省 $i$ 的每个参赛者都会站在方格$（i，p）$中，并满足 $L_i\leq p\leq R_i$ 。因此，我们可以看到有 $R_i-L_i+1$ 个参赛者代表省 $i$ 。 PC 的变量 $Z$ 最初等于 $0$ 。在一次操作中，PC 可以选择行 $i$ 和正整数 $k$ 。然后，PC 将执行以下两种操作之一： - 将第 $i$ 行中的所有参赛者向西移动 $k$ 个方格。换句话说，在 $(i,p)$ 中的选手被移动到 $(i,p-k)$。 - 将第 $i$ 行中的所有参赛者向东移动 $k$ 个方格。换句话说，在 $(i,p)$ 中的选手被移动到 $(i,p+k)$。 每次操作后，$Z$的值将变为$Z~\text{OR}~k$，其中$\text{OR}$是按位或运算. 请注意，PC 可以多次对同一行执行操作。还要注意，PC 不允许将参赛者移出网格。 有 $Q$ 问题。对于第 $j$ 个问题，您将得到一个正整数 $W_j $，PC 必须执行零或更多操作，以便 $Z$ 的最终值正好是 $W_j$ 。将 $M$ 定义为最大的数字，以便在所有操作之后，至少有一列正好包含 $M$ 参赛者。对于每个问题，您必须找到 PC 可以完成的所有操作序列的最大可能 $M$ 。请注意，PC 针对一个问题所做的操作不会延续到其他问题。

第一行包含一个整数$N(1\leq N\leq 10^5)~~$ 即网格中的行数以及参与 OSN 2019 的省份数。 接下来 $N$ 行的第 $i$ 行包含两个整数 $L_i$ 和 $R_i~~(1\leq L_i\leq R_i\leq 10^9)$ ，描述代表省 $i$ 的参赛者的位置。 下一行包含将询问的问题数 $Q$（$1\leq Q\leq 10^5$）。 接下来 $Q$ 行的第 $j$ -行包含一个整数$W_j$（$1\leq W_j\leq 10^9$）即第$j$个问题所需的最终值$Z$。

输出 $Q$ 行，第 $j$ 行包含一个整数，即第 $j$ 个问题中 $M$ 的最大值。

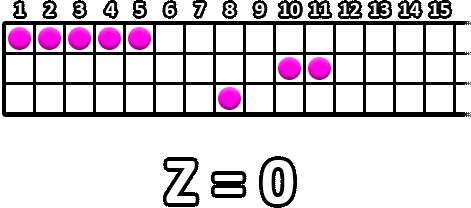
对于第 $1$ 个问题，PC 可以执行以下操作以获得 $M=2$： - 将第 $2$ 排中的所有参赛者向东移动 $4$ 块 $Z$ 变为$0~\text{OR}~4=4$。 - 将第 $1$ 排中的所有参赛者向东移动$12$块$Z$变为$4~\text{OR}~12=12$。 现在，每列 $14$ 和 $15$ 正好包含 $2$ 的参赛者。 对于第二个 $2$ 问题，PC可以执行以下操作以获得 $M=3$： - 将第 $3$ 排中的所有参赛者向东移动 $4$ 块 $Z$ 变为$0~\text{OR}~4=4$。 - 将第 $3$ 排中的所有参赛者向西移动 $1$ 行 $Z$ 变为 $4~\text{OR}~1=5$。 - 将 $1$ 排中的所有参赛者向东移动$5$块$Z$变为$5~\text{OR}~5=5$。 - 将 $1$ 排中的所有参赛者向东移动 $5$ 块 $Z$ 变为 $5~\text {OR}~5=5$。 现在，第 $11$ 列正好包含 $3$ 名参赛者。 下面是第 $2$ 个问题的示例操作说明。