CF1725I Imitating the Key Tree

Pak Chanek 有一棵密钥树。这棵树包含 $N$ 个顶点和 $N - 1$ 条边。这些边按照 $1$ 到 $N - 1$ 连接着 $U_i$ 和 $V_i$。最开始，所有边都没有权值。 长度是 $k$ 的路径可以看成这样： $[v_1, e_1, v_2, e_2, v_3, e_3, \ldots, v_k, e_k, v_{k+1}]$ 而且满足以下条件。 - 对于每个 $ i $ , $ v_i $ 是一个顶点且 $ e_i $ 是一条边。 - 对于每个 $ i $ , $ e_i $ 连接了顶点 $ v_i $ 和 $ v_{i+1} $ . 一个环就是一个路径开始和结束顶点相同。 当且仅当路径不多次使用同一条边时，图中的路径称为简单。请注意，简单路径可以多次使用同一顶点。 有权图中简单路径的权重为它所遍历的所有边的最大权重。 要求计算满足以下条件的不同无向带权图的数量： - 图有 $ N $ 个顶点和 $ 2N-2 $ 条边. - 对于每一对顶点 $ (x, y) $ , 一定有一条简单环路通过了 $ x $ 和 $ y $。 - 每条边的权重为 $ 1 $ 到 $ 2N-2 $ 的一个整数，而且每条边的权重不同。 - 该图可以这样的方式生成，即有一种方法将权重 $W_i$ 分配给满足以下条件的密钥树中的每个边$i$： - 对于每一对边 $ (i, j) $ , 如果 $ i

第一行包含了一个整数 $N$，代表顶点的个数。 接下来 $N - 1$ 行中的第 $i$ 行包含了两个整数 $ U_i $ 和 $ V_i $ ，表示一条连接 $U_i$ 和 $V_i$ 的边。

一个整数表示满足问题条件的不同无向带权图的数目对$ 998\,244\,353 $ 取模的结果。 #### 样例 #1 ##### 样例输入 #1 ``` 4 3 2 1 3 4 3 ``` ##### 样例输出 #1 ``` 540 ```

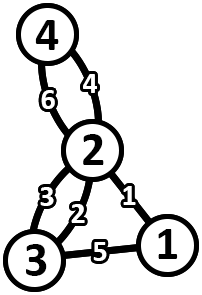
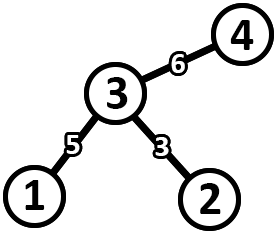
以下是满足条件的图的示例。  以下是对应于上图的关键树中边权重的分配。  例如，考虑一对顶点索引 $ (1, 4) $ . - 这对顶点的环路是 $ 3 \xrightarrow{2} 2 \xrightarrow{4} 4 \xrightarrow{6} 2 \xrightarrow{1} 1 \xrightarrow{5} 3 $ ，花费为 $ 6 $ . - 这对顶点的路径为： $ 1 \xrightarrow{5} 3 \xrightarrow{6} 4 $ 花费为 $ 6 $ . 对于 $100\%$ 的样例，$ 2 \le N \le 10^5 ， 1 \le U_i, V_i \le N 。$