CF1725I Imitating the Key Tree

Pak Chanek has a tree called the key tree. This tree consists of $ N $ vertices and $ N-1 $ edges. The edges of the tree are numbered from $ 1 $ to $ N-1 $ with edge $ i $ connecting vertices $ U_i $ and $ V_i $ . Initially, each edge of the key tree does not have a weight. Formally, a path with length $ k $ in a graph is a sequence $ [v_1, e_1, v_2, e_2, v_3, e_3, \ldots, v_k, e_k, v_{k+1}] $ such that: - For each $ i $ , $ v_i $ is a vertex and $ e_i $ is an edge. - For each $ i $ , $ e_i $ connects vertices $ v_i $ and $ v_{i+1} $ . A circuit is a path that starts and ends on the same vertex. A path in a graph is said to be simple if and only if the path does not use the same edge more than once. Note that a simple path can use the same vertex more than once. The cost of a simple path in a weighted graph is defined as the maximum weight of all edges it traverses. Count the number of distinct undirected weighted graphs that satisfy the following conditions: - The graph has $ N $ vertices and $ 2N-2 $ edges. - For each pair of different vertices $ (x, y) $ , there exists a simple circuit that goes through vertices $ x $ and $ y $ in the graph. - The weight of each edge in the graph is an integer between $ 1 $ and $ 2N-2 $ inclusive. Each edge has distinct weights. - The graph is formed in a way such that there is a way to assign a weight $ W_i $ to each edge $ i $ in the key tree that satisfies the following conditions: - For each pair of edges $ (i, j) $ , if $ i

The first line contains a single integer $ N $ ( $ 2 \le N \le 10^5 $ ) — the number of vertices in the key tree. The $ i $ -th of the next $ N-1 $ lines contains two integers $ U_i $ and $ V_i $ ( $ 1 \le U_i, V_i \le N $ ) — an edge connecting vertices $ U_i $ and $ V_i $ . The graph in the input is a tree.

An integer representing the number of distinct undirected weighted graphs that satisfy the conditions of the problem modulo $ 998\,244\,353 $ .

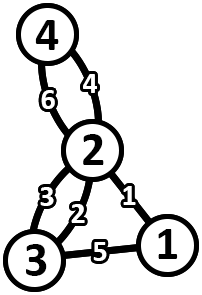
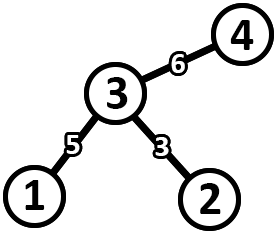
The following is an example of a graph that satisfies.  The following is an assignment of edge weights in the key tree that corresponds to the graph above.  As an example, consider a pair of vertex indices $ (1, 4) $ . - The circuit in the graph for this pair of vertices is $ 3 \xrightarrow{2} 2 \xrightarrow{4} 4 \xrightarrow{6} 2 \xrightarrow{1} 1 \xrightarrow{5} 3 $ with a cost of $ 6 $ . - The path in the key tree for this pair of vertices is $ 1 \xrightarrow{5} 3 \xrightarrow{6} 4 $ with a cost of $ 6 $ .