CF1726C Jatayu's Balanced Bracket Sequence

### 题目大意 对于一个长度为 $2n$ 的**合法**的括号串 $s$，按照如下方法构造一张无向图： - 括号序列的所有位置都是无向图中的一个点。 - 对于该序列的任意位置 $l$，它能向另一个位置 $r$ 连边当且仅当满足子串 $s[l, \; \dots , \; r]$ 也是一个**合法**括号串。 求这张无向图的连通块个数。

第一行包含一个整数 $T \; (1 \leqslant T \leqslant 10^5)$ 表示测试样例组数。 对于每组测试样例，第一行包含一个整数 $n \; (1 \leqslant n \leqslant 10^5)$ 表示序列长度为 $2n$。 接下来的一行包含一个长度为 $2n$ 的合法括号串。

对于每组测试样例，包含一个整数表示该串构造的无向图的连通块数。 $Translated \; by \; Zigh$

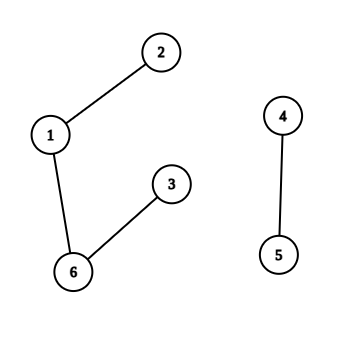
Sample explanation: In the first test case, the graph constructed from the bracket sequence (), is just a graph containing nodes $ 1 $ and $ 2 $ connected by a single edge. In the second test case, the graph constructed from the bracket sequence ()(()) would be the following (containing two connected components): Definition of Underlined Terms: - A sequence of brackets is called balanced if one can turn it into a valid math expression by adding characters $ + $ and $ 1 $ . For example, sequences (())(), (), and (()(())) are balanced, while )(, ((), and (()))( are not. - The subsegment $ s[l \ldots r] $ denotes the sequence $ [s_l, s_{l + 1}, \ldots, s_r] $ . - A connected component is a set of vertices $ X $ such that for every two vertices from this set there exists at least one path in the graph connecting these vertices, but adding any other vertex to $ X $ violates this rule.