CF1726H Mainak and the Bleeding Polygon
题目描述
### **题目大意**
以逆时针顺序给出笛卡尔平面上 $n (4 \leqslant n \leqslant 5000)$ 个点 $A_1,A_2,...,A_n$ 的坐标,从而确定一凸多边形。该凸多边形的性质有如下保证:
- 所有点的坐标均为整数且 $-10^{9} \leqslant x,y \leqslant 10^{9}$ 。
- 对于该凸多边形的任意内角 $\alpha$ ,均有 $90^{\circ} \leqslant \alpha < 180^{\circ}$ 。
现从凸多边形的任意两边上分别取出两点,将所有由两点所确定的、长度不超过 $1$ 的弦所经过的凸多边形内部区域**标红**。求标红区域的面积。
输入格式
第一行输入 $n$ 。
之后 $n$ 行每行给出 $1$ 个点的坐标。
输出格式
只输出标红区域的面积,保留 $11$ 位小数。误差不超过 $10^{-4}$ 即视为正确。
说明/提示
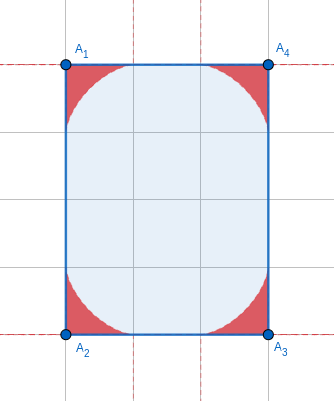
In the first example, the polygon $ \mathcal P $ can be visualised on the Cartesian Plane as: