CF1726H Mainak and the Bleeding Polygon

Mainak has a convex polygon $ \mathcal P $ with $ n $ vertices labelled as $ A_1, A_2, \ldots, A_n $ in a counter-clockwise fashion. The coordinates of the $ i $ -th point $ A_i $ are given by $ (x_i, y_i) $ , where $ x_i $ and $ y_i $ are both integers. Further, it is known that the interior angle at $ A_i $ is either a right angle or a proper obtuse angle. Formally it is known that: - $ 90 ^ \circ \le \angle A_{i - 1}A_{i}A_{i + 1} < 180 ^ \circ $ , $ \forall i \in \{1, 2, \ldots, n\} $ where we conventionally consider $ A_0 = A_n $ and $ A_{n + 1} = A_1 $ . Mainak's friend insisted that all points $ Q $ such that there exists a chord of the polygon $ \mathcal P $ passing through $ Q $ with length not exceeding $ 1 $ , must be coloured $ \color{red}{\text{red}} $ . Mainak wants you to find the area of the coloured region formed by the $ \color{red}{\text{red}} $ points. Formally, determine the area of the region $ \mathcal S = \{Q \in \mathcal{P} $ | $ Q \text{ is coloured } \color{red}{\text{red}}\} $ . Recall that a chord of a polygon is a line segment between two points lying on the boundary (i.e. vertices or points on edges) of the polygon.

The first line contains an integer $ n $ ( $ 4 \le n \le 5000 $ ) — the number of vertices of a polygon $ \mathcal P $ . The $ i $ -th line of the next $ n $ lines contain two integers $ x_i $ and $ y_i $ ( $ -10^9 \le x_i, y_i \le 10^9 $ ) — the coordinates of $ A_i $ . Additional constraint on the input: The vertices form a convex polygon and are listed in counter-clockwise order. It is also guaranteed that all interior angles are in the range $ [90^\circ ; 180^\circ ) $ .

Print the area of the region coloured in $ \color{red}{\text{red}} $ . Your answer is considered correct if its absolute or relative error does not exceed $ 10^{-4} $ . Formally, let your answer be $ a $ , and the jury's answer be $ b $ . Your answer is accepted if and only if $ \frac{|a - b|}{\max{(1, |b|)}} \le 10^{-4} $ .

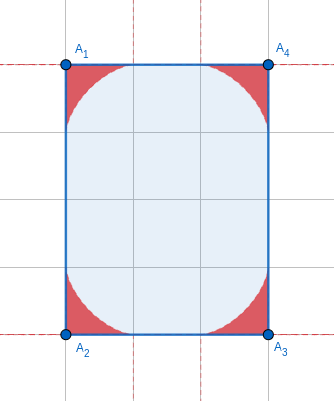
In the first example, the polygon $ \mathcal P $ can be visualised on the Cartesian Plane as: