CF1729C Jumping on Tiles

### 题目大意 给定一个字符串 $s$，polycarp 欲从字符串首跳到字符串末 ($s_1$ → $s_n$，其中 $n$ 表示该字符串长度)。 假设 polycarp 现从 $a_i$ 跳到了 $a_j$ 我们定义这一次跳跃的权值为 $|\operatorname{index}(a_i) - \operatorname{index}(a_j)|$，其中 $\operatorname{index}$ 表示该字符在字母表中的序号 ( 如 $\operatorname{index}('a') = 1, \; \operatorname{index}('z') = 26$ )。 请构造出一种在保证**权值和最小**的情况下**经过的字符最多**的跳跃方案 ( 当然，同一个字符只能经过一次，其中同一个仅指在字符串中的位置相同 )。

第一行包含一个整数 $t \; (1 \leqslant t \leqslant 10^4)$ ，表示测试样例组数。 对于每组测试样例，包含一行一个字符串 $s \; (2 \leqslant |s| \leqslant 2 \cdot 10^5)$，意义见题面。

对于每组测试样例，第一行包含两个用空格隔开的整数 $cost$ 和 $m$ 分别表示 最小权值和 和 最大经过的字符数。 第二行包含 $m$ 个整数，分别表示沿途经过的所有字符位置。( 例如输出 $1 \; 4 \; 3 \; 5$ 表示跳跃路径为 $s_1$ → $s_4$ → $s_3$ → $s_5$ ) 数与数之间用空格隔开。 $Translated \; by \; Zigh$

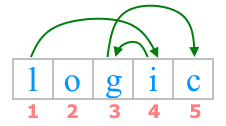In the first test case, the required path corresponds to the picture: In this case, the minimum possible total cost of the path is achieved. Since $ index( $ 'l' $ )=12 $ , $ index( $ 'o' $ )=15 $ , $ index( $ 'g' $ )=7 $ , $ index( $ 'i' $ )=9 $ , $ index( $ 'c' $ )=3 $ , then the total cost of the path is $ |12-9|+|9-7|+|7-3|=3+2+4=9 $ .