CF172B Pseudorandom Sequence Period

Polycarpus has recently got interested in sequences of pseudorandom numbers. He learned that many programming languages generate such sequences in a similar way: 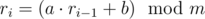 (for $ i>=1 $ ). Here $ a $ , $ b $ , $ m $ are constants, fixed for the given realization of the pseudorandom numbers generator, $ r_{0} $ is the so-called $ randseed $ (this value can be set from the program using functions like RandSeed(r) or srand(n)), and 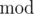 denotes the operation of taking the remainder of division. For example, if $ a=2,b=6,m=12,r_{0}=11 $ , the generated sequence will be: $ 4,2,10,2,10,2,10,2,10,2,10,... $ . Polycarpus realized that any such sequence will sooner or later form a cycle, but the cycle may occur not in the beginning, so there exist a preperiod and a period. The example above shows a preperiod equal to 1 and a period equal to 2. Your task is to find the period of a sequence defined by the given values of $ a,b,m $ and $ r_{0} $ . Formally, you have to find such minimum positive integer $ t $ , for which exists such positive integer $ k $ , that for any $ i>=k $ : $ r_{i}=r_{i+t} $ .

The single line of the input contains four integers $ a $ , $ b $ , $ m $ and $ r_{0} $ ( $ 1

Print a single integer — the period of the sequence.

The first sample is described above. In the second sample the sequence is (starting from the first element): $ 0,3,4,1,0,3,4,1,0,... $ In the third sample the sequence is (starting from the first element): $ 33,24,78,78,78,78,... $