CF1733E Conveyor

有一个 $120$ 行，$120$ 列的棋盘，行列编号均为 $0,1,\cdots,119$，$i$ 行 $j$ 列的格子的坐标为 $(i,j)$，左上角的格子坐标为 $(0,0)$。每一个格子上都有一个传送带，初始方向为右。 一开始，有一个史莱姆在 $(0,0)$，其他格子都什么也没有，每一秒传送带的方向都会如下变化： - 所有的史莱姆随着传送带的方向移动一格。如果传送带的方向没有格子，史莱姆就会离开棋盘；如果两个史莱姆到了同一个格子上，就会合并为一个史莱姆。 - 所有**上一秒**有史莱姆的传送带的方向都会改变，向右的会变成向下的，向下的会变成向右的。 - $(0,0)$ 处会出现一个史莱姆。 给定 $q$ 个询问，问在第 $t$ 秒，$(x,y)$ 格是否有史莱姆。

第一行，一个整数 $q$（ $1\le q\le10^4$ ），表示询问个数。 每一行询问依次有三个整数 $t,x,y$（$0\le t\le10^{18},0\le x,y

如果在第 $t$ 秒，$(x,y)$ 格有史莱姆，输出 `YES`，否则输出 `NO`。

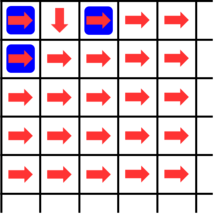
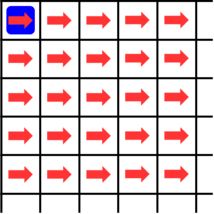
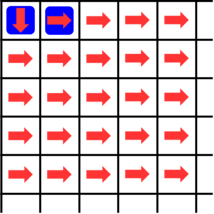
$ t = 0 $ 时的棋盘如图。红色箭头表示每个传送带的方向，蓝色图案表示史莱姆。  $ t = 1 $ 时的棋盘如图。  $ t = 2 $ 时的棋盘如图。