CF1735C Phase Shift

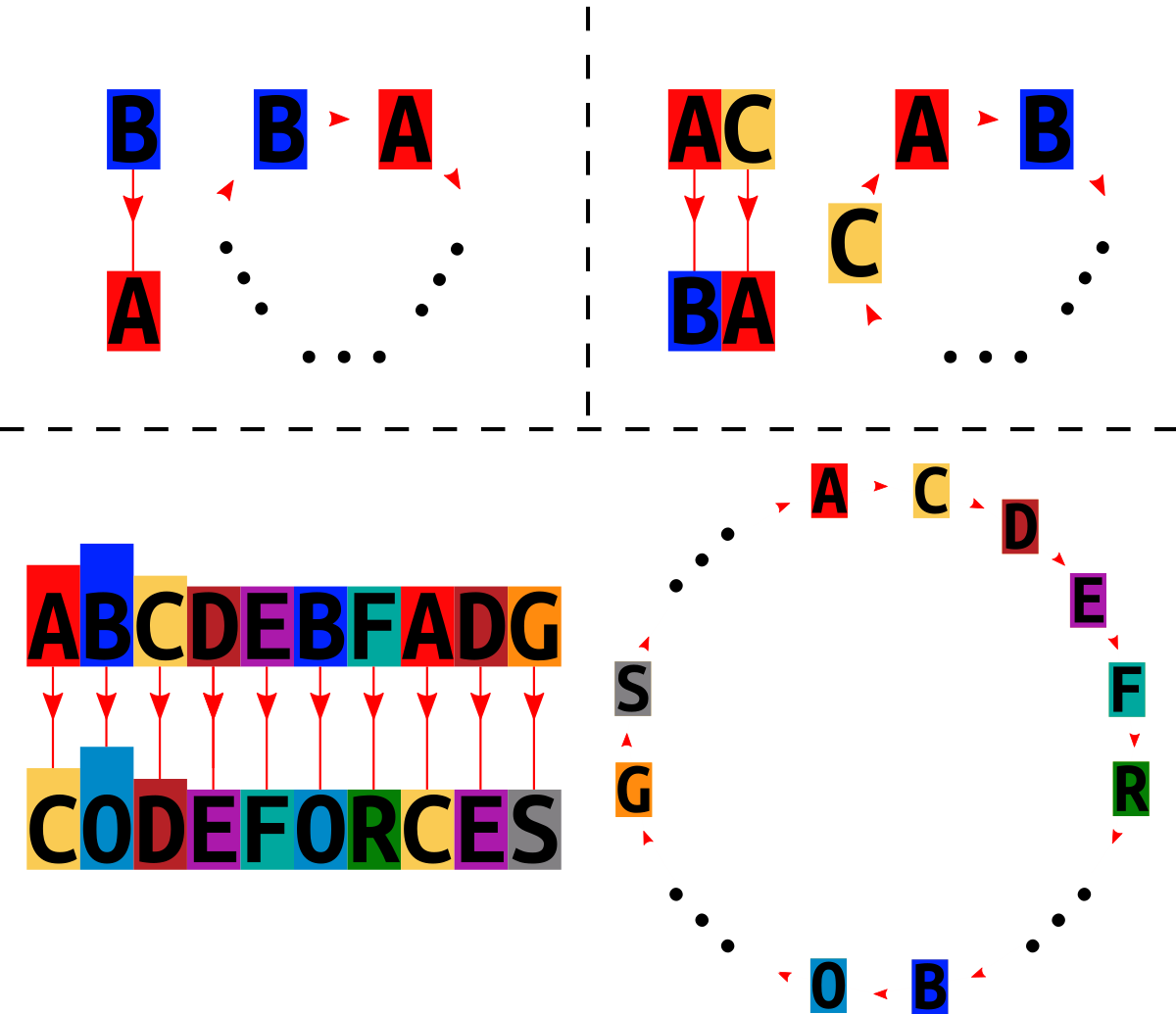
There was a string $ s $ which was supposed to be encrypted. For this reason, all $ 26 $ lowercase English letters were arranged in a circle in some order, afterwards, each letter in $ s $ was replaced with the one that follows in clockwise order, in that way the string $ t $ was obtained. You are given a string $ t $ . Determine the lexicographically smallest string $ s $ that could be a prototype of the given string $ t $ . A string $ a $ is lexicographically smaller than a string $ b $ of the same length if and only if: - in the first position where $ a $ and $ b $ differ, the string $ a $ has a letter, that appears earlier in the alphabet than the corresponding letter in $ b $ .

The first line of the input contains a single integer $ t $ ( $ 1 \le t \le 3 \cdot 10^4 $ ) — the number of test cases. The description of test cases follows. The first line of each test case contains one integer $ n $ ( $ 1 \le n \le 10^5 $ ) — the length of the string $ t $ . The next line contains the string $ t $ of the length $ n $ , containing lowercase English letters. It is guaranteed that the sum of $ n $ over all test cases doesn't exceed $ 2 \cdot 10^5 $ .

For each test case, output a single line containing the lexicographically smallest string $ s $ which could be a prototype of $ t $ .

In the first test case, we couldn't have the string "a", since the letter a would transit to itself. Lexicographically the second string "b" is suitable as an answer. In the second test case, the string "aa" is not suitable, since a would transit to itself. "ab" is not suitable, since the circle would be closed with $ 2 $ letters, but it must contain all $ 26 $ . The next string "ac" is suitable. Below you can see the schemes for the first three test cases. The non-involved letters are skipped, they can be arbitrary placed in the gaps.