CF1735D Meta-set

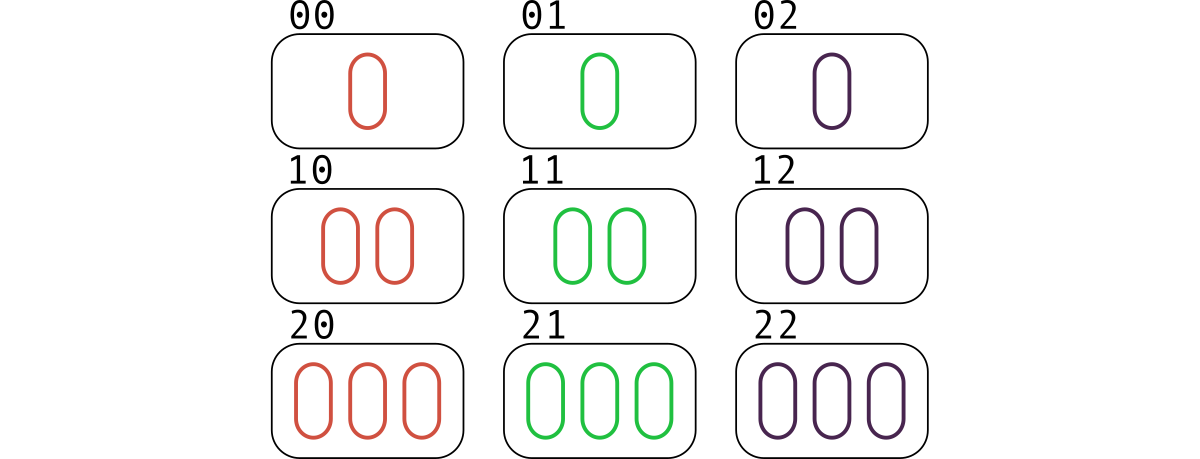
You like the card board game "Set". Each card contains $ k $ features, each of which is equal to a value from the set $ \{0, 1, 2\} $ . The deck contains all possible variants of cards, that is, there are $ 3^k $ different cards in total. A feature for three cards is called good if it is the same for these cards or pairwise distinct. Three cards are called a set if all $ k $ features are good for them. For example, the cards $ (0, 0, 0) $ , $ (0, 2, 1) $ , and $ (0, 1, 2) $ form a set, but the cards $ (0, 2, 2) $ , $ (2, 1, 2) $ , and $ (1, 2, 0) $ do not, as, for example, the last feature is not good. A group of five cards is called a meta-set, if there is strictly more than one set among them. How many meta-sets there are among given $ n $ distinct cards?

The first line of the input contains two integers $ n $ and $ k $ ( $ 1 \le n \le 10^3 $ , $ 1 \le k \le 20 $ ) — the number of cards on a table and the number of card features. The description of the cards follows in the next $ n $ lines. Each line describing a card contains $ k $ integers $ c_{i, 1}, c_{i, 2}, \ldots, c_{i, k} $ ( $ 0 \le c_{i, j} \le 2 $ ) — card features. It is guaranteed that all cards are distinct.

Output one integer — the number of meta-sets.

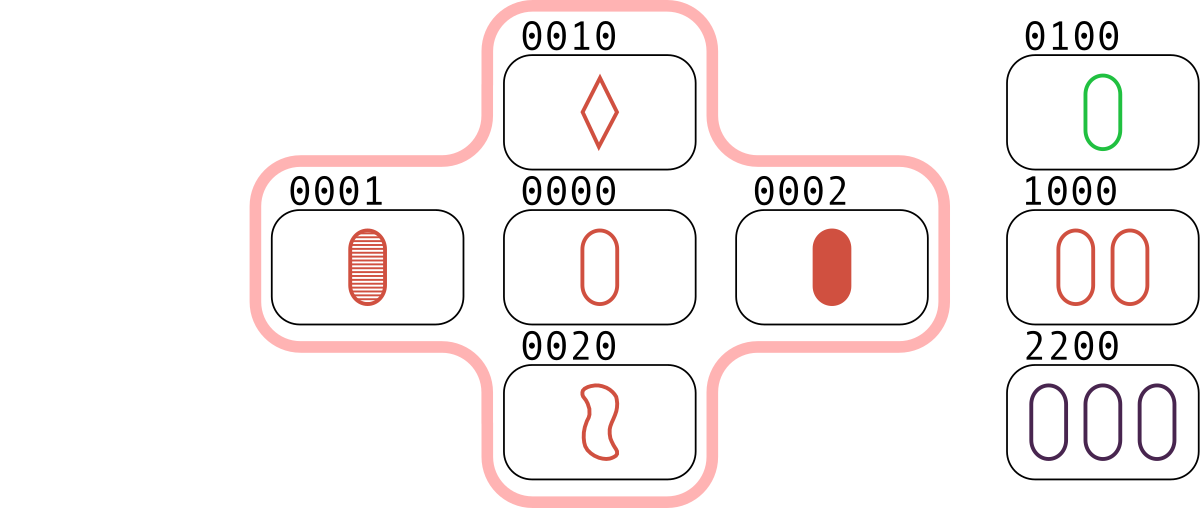
Let's draw the cards indicating the first four features. The first feature will indicate the number of objects on a card: $ 1 $ , $ 2 $ , $ 3 $ . The second one is the color: red, green, purple. The third is the shape: oval, diamond, squiggle. The fourth is filling: open, striped, solid. You can see the first three tests below. For the first two tests, the meta-sets are highlighted. In the first test, the only meta-set is the five cards $ (0000,\ 0001,\ 0002,\ 0010,\ 0020) $ . The sets in it are the triples $ (0000,\ 0001,\ 0002) $ and $ (0000,\ 0010,\ 0020) $ . Also, a set is the triple $ (0100,\ 1000,\ 2200) $ which does not belong to any meta-set. 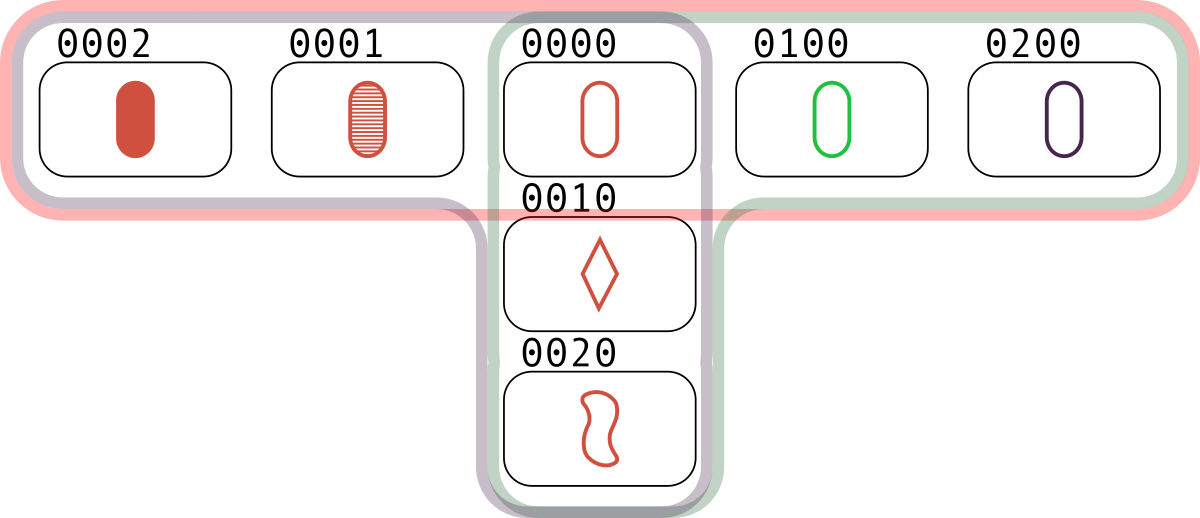In the second test, the following groups of five cards are meta-sets: $ (0000,\ 0001,\ 0002,\ 0010,\ 0020) $ , $ (0000,\ 0001,\ 0002,\ 0100,\ 0200) $ , $ (0000,\ 0010,\ 0020,\ 0100,\ 0200) $ . In there third test, there are $ 54 $ meta-sets.