CF1735D Meta-set

### 题目翻译 你有一副牌，每张牌包含$k$个特征，每个特征等于集合 $\{0，1，2\}$ 中的一个值。显然，共有$3^k$ 不同的情况。 定义一个三张牌为好的，当且仅当：对于同一位上的特征，要么**相同**，要么**两两不同**。如果**三张牌**所有$k$对特征都是好的，则称为一个集合。 如果一组**五张牌**中有严格意义上的**一个以上**的集合，则称为元组。在给定的$n$个不同的牌中，有多少个元组？

输入的第一行包含两个整数 $n$ 和 $k$ $( 1\le n\le 10^3)$ $( 1 \le k \le 20）$,表示桌子上的牌的数量和牌的特征的数量。在接下来的$n$行中，将对牌进行描述。 描述卡片的每一行包含$k$个整数，表示卡片特征$\{0，1，2\}$。所有卡片都是**不同的**。

输出一个整数表示元组的数量。

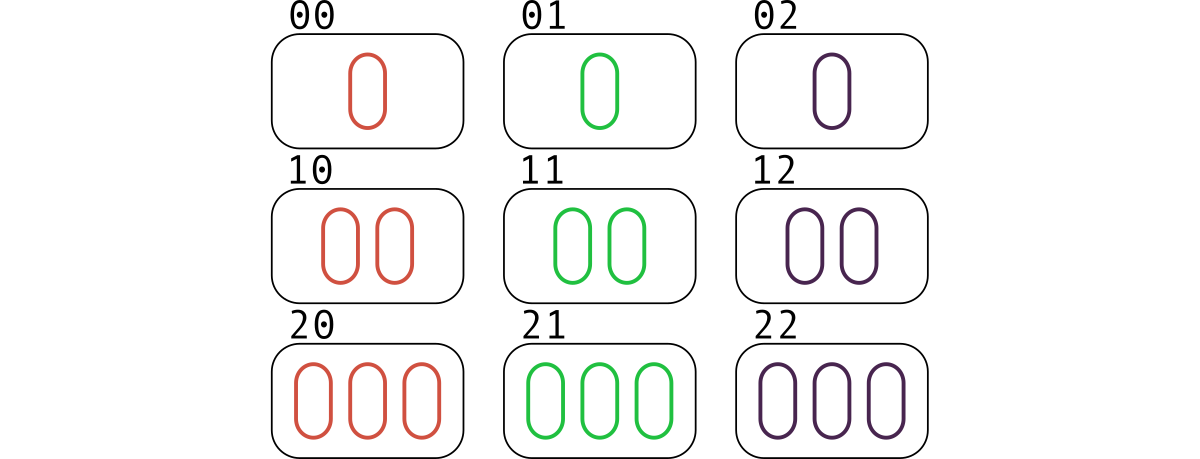
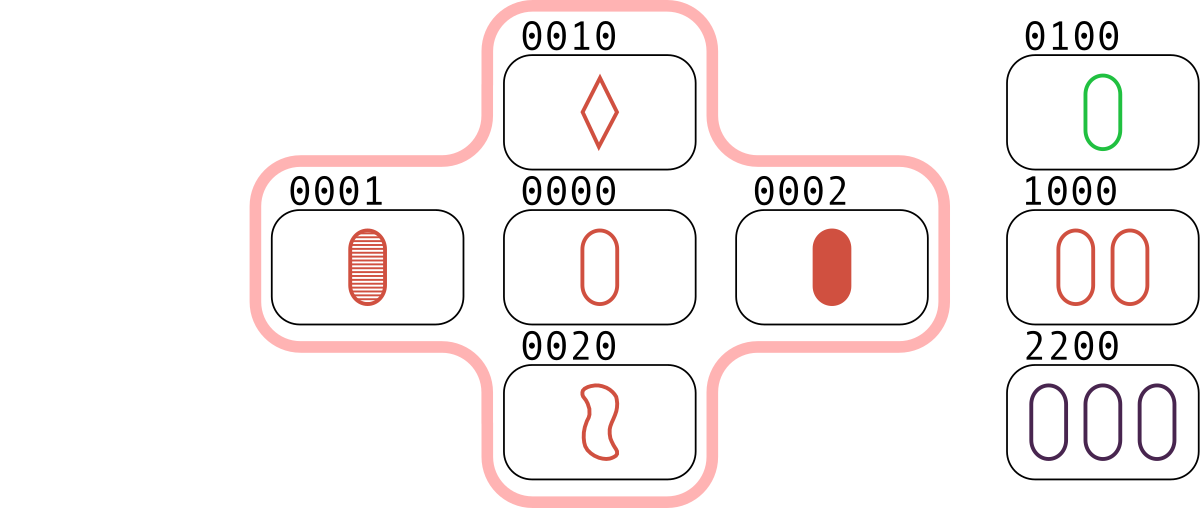
Let's draw the cards indicating the first four features. The first feature will indicate the number of objects on a card: $ 1 $ , $ 2 $ , $ 3 $ . The second one is the color: red, green, purple. The third is the shape: oval, diamond, squiggle. The fourth is filling: open, striped, solid. You can see the first three tests below. For the first two tests, the meta-sets are highlighted. In the first test, the only meta-set is the five cards $ (0000,\ 0001,\ 0002,\ 0010,\ 0020) $ . The sets in it are the triples $ (0000,\ 0001,\ 0002) $ and $ (0000,\ 0010,\ 0020) $ . Also, a set is the triple $ (0100,\ 1000,\ 2200) $ which does not belong to any meta-set. 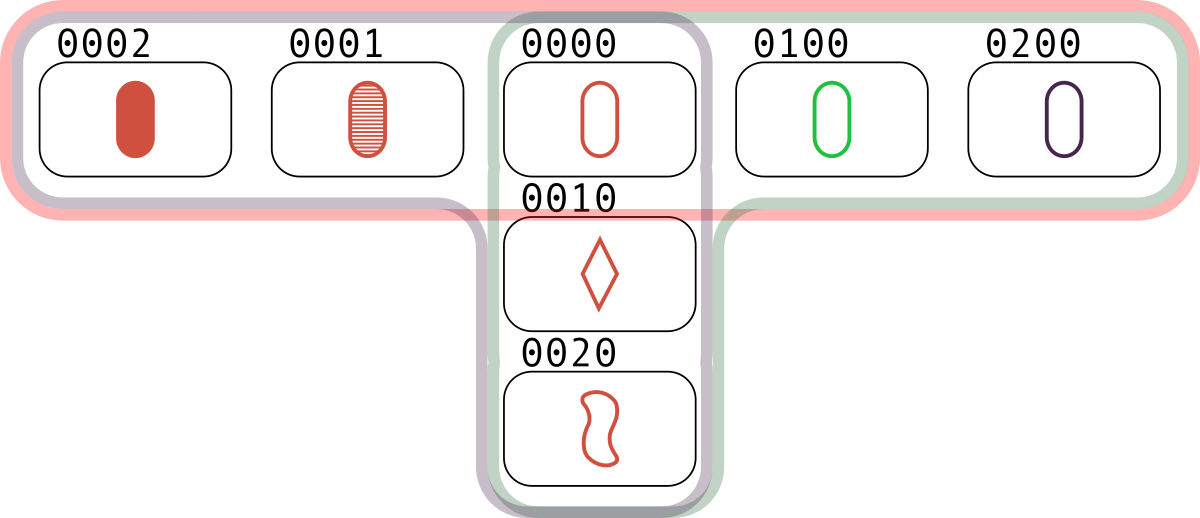In the second test, the following groups of five cards are meta-sets: $ (0000,\ 0001,\ 0002,\ 0010,\ 0020) $ , $ (0000,\ 0001,\ 0002,\ 0100,\ 0200) $ , $ (0000,\ 0010,\ 0020,\ 0100,\ 0200) $ . In there third test, there are $ 54 $ meta-sets.