CF1735E House Planning

你的城市中有 $n$ 座房屋，沿一条轴线排列在点 $h_1, h_2, \ldots, h_n$ 上。你想为自己建一座新房子，并考虑将其建在两个备选位置之一：点 $p_1$ 和 $p_2$。 由于你喜欢拜访朋友，你提前计算了从这两个备选位置到所有现有房屋的距离。更正式地说，你计算了两个数组 $d_1$、$d_2$：$d_{i, j} = |p_i - h_j|$，其中 $|x|$ 表示 $x$ 的绝对值。 经过很长时间后，你忘记了房屋 $h$ 和备选位置 $p_1$、$p_2$ 的具体位置。但你的日记中仍然保留着这两个数组——$d_1$ 和 $d_2$，但你怀疑它们的真实性。此外，每个数组中的值可能已经被打乱，因此 $d_1$ 和 $d_2$ 中相同位置的值可能对应不同的房屋。请注意，一个数组中的值不会出现在另一个数组中，换句话说，$d_1$ 中的所有值都对应从 $p_1$ 到各房屋的距离，$d_2$ 中的所有值都对应从 $p_2$ 到各房屋的距离。 还要注意，房屋 $h_i$ 和备选点 $p_j$ 的位置可能重合。例如，以下位置是合法的：$h = \{1, 0, 3, 3\}$，$p = \{1, 1\}$，这可能对应已经打乱的 $d_1 = \{0, 2, 1, 2\}$，$d_2 = \{2, 2, 1, 0\}$。 请判断是否存在一组房屋 $h$ 和备选点 $p_1$、$p_2$ 的位置，使得给定的距离数组是正确的。如果可能，请给出一种可行的房屋和备选点的位置。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^3$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 10^3$），表示数组 $d_1$ 和 $d_2$ 的长度。 接下来的两行，每行包含 $n$ 个整数，分别为数组 $d_1$ 和 $d_2$（$0 \le d_{i, j} \le 10^9$）。 保证所有测试用例中 $n$ 的总和不超过 $2 \times 10^3$。

对于每个测试用例，如果无解，输出一行 "NO"。 否则输出三行。第一行输出 "YES"。第二行输出 $n$ 个整数 $h_1, h_2, \ldots, h_n$。第三行输出两个整数 $p_1$ 和 $p_2$。 要求满足 $0 \le h_i, p_1, p_2 \le 2 \times 10^9$。可以证明，如果有解，则一定存在满足这些约束的解。 如果有多组解，输出任意一组均可。

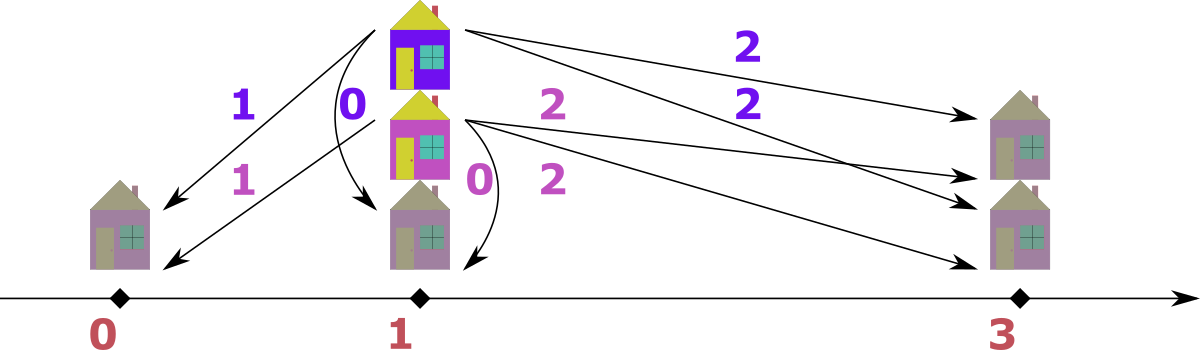
下图展示了样例的解。计划建造的房屋用亮色表示：粉色和紫色。现有房屋用暗色表示。 在第 $1$ 个测试用例中，第一个计划房屋位于 $0$ 点，第二个位于 $10$ 点。现有房屋位于 $5$ 点，距离两个计划房屋的距离都是 $5$。 可以证明第 $2$ 个测试用例无解。 在第 $3$ 个测试用例中，计划房屋分别位于 $33$ 和 $69$ 点。 注意在第 $4$ 个测试用例中，两个计划点都位于 $1$ 点，同时有一座现有房屋也在该点。这是一个合法的方案。  由 ChatGPT 4.1 翻译