CF1735F Pebbles and Beads

这里有两种货币：鹅卵石和珠子。最初你有 $a$ 颗鹅卵石和 $b$ 个珠子。 一共有 $n$ 天，每天你可以按照某个汇率将一种货币兑换成另一种货币。 在第 $i$ 天，你可以通过交换 $-p_i \leq x \leq p_i$ 来获得 $-q_i \leq y \leq q_i$ 的珠子或者相反。允许不进行任何交换。同时，如果你进行了交换，必须满足比例 $x \cdot q_i =-y\cdot p_i$。允许进行小数交换。 你一天只能进行一次这样的交换。你拥有的鹅卵石和珠子的数量必须始终保持非负。 请解决以下 $n$ 个问题：对于第 $i$ 天，输出在进行最优交换后，第 $i$ 天结束时你可以拥有的最大鹅卵石数量。 ### **简明题意** 你初始有 $a$ 个鹅卵石和 $b$ 个珠子。对于给定的 $n$ 天的汇率，请求出每天结束后能拥有的最大鹅卵石数量。

第一行输入三个整数 $n,a,b$ $(1\le n\le 300000,0\le a,b\le 10^9)$，分别表示一共有几天，初始的鹅卵石数量和珠子数量。 第二行输入 $n$ 个整数 $p_1,p_2,...,p_n$。 第三行输入 $n$ 个整数 $q_1,q_2,...,q_n$ $(1\le q_i\le 10^9)$。 保证每组数据 $n$ 的总和不超过 $300000$。

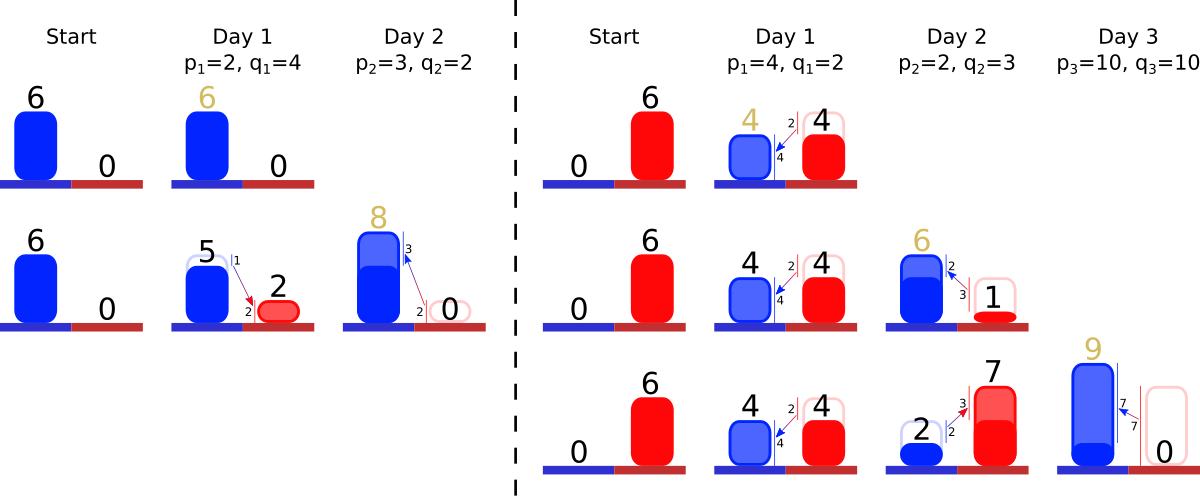
输出 $n$ 个整数，表示每天结束后鹅卵石最多有多少个。 答案误差可以在 $10^{-6}$ 之内。 更正规地说，如果你的答案是 $a$，标准答案是 $b$，那么你的答案会被认为是正确的当且仅当 $\dfrac{\left\vert{a-b}\right\vert}{\max(1,\left\vert{b}\right\vert)}\le 10^{-6}$。 ### **说明/提示** 在下图中你能看见前两组数据的解决方案。每一行都是每天的最佳行动序列。 第一组数据中，第一天的最佳策略是不采取任何行动，因为我们只能减少鹅卵石的数量。第二天的最佳策略是首先交换 $1$ 颗鹅卵石换取 $2$ 颗珠子，这是一个正确的交换，因为 $1 \cdot 4 = 2 \cdot 2$，然后再用 $2$ 颗珠子换取 $3$ 颗鹅卵石。

In the image below you can see the solutions for the first two test cases. In each line there is an optimal sequence of actions for each day. In the first test case, the optimal strategy for the first day is to do no action at all, as we can only decrease the number of pebbles. The optimal strategy for the second day is at first to exchange $ 1 $ pebble for $ 2 $ beads, which is a correct exchange, since $ 1 \cdot 4 = 2 \cdot 2 $ , and then to exchange $ 2 $ beads for $ 3 $ pebbles.