CF1737E Ela Goes Hiking

Ela 非常喜欢远足。她热爱大自然，喜欢探索各种生物。有一天，她看到了一种奇怪的蚂蚁，这种蚂蚁具有食同类的特性。更具体地说，一只蚂蚁会吃掉它看到的比自己小的任何蚂蚁。Ela 对这种新生物的特性感到好奇，但并不生气。她进行了一项漫长、严谨且富有感情的实验。 她将 $n$ 只食同类的蚂蚁排成一行，放在一根长木棍上。最初，每只蚂蚁的重量都是 $1$。任意两只相邻蚂蚁之间的距离相同。队列中第一只蚂蚁到木棍左端的距离，以及最后一只蚂蚁到木棍右端的距离，也与蚂蚁之间的距离相同。每只蚂蚁开始时会随机且等概率地向左端或右端移动，并且在整个实验过程中以相同的恒定速度移动。当两只蚂蚁相邻且朝相反方向移动时会相遇碰撞，蚂蚁到达木棍两端时会立即改变方向。Ela 无法确定每只蚂蚁的初始移动方向，但她非常了解它们在碰撞时的行为。 - 如果两只蚂蚁碰撞时重量不同，则较重的蚂蚁会吃掉较轻的蚂蚁，并获得较轻蚂蚁的重量。之后，较重的蚂蚁会继续朝原方向行走。换句话说，如果较重的蚂蚁重量为 $x$ 并向右走，较轻的蚂蚁重量为 $y$ 并向左走（$x > y$），那么碰撞后，较轻的蚂蚁会消失，较重的蚂蚁的重量变为 $x + y$，并继续向右走。 - 如果两只蚂蚁碰撞时重量相同，则向左走的蚂蚁会吃掉向右走的蚂蚁，并继续朝原方向行走。换句话说，如果一只重量为 $x$ 的蚂蚁向左走，与另一只重量为 $x$ 的蚂蚁向右走相遇，向右走的蚂蚁会消失，向左走的蚂蚁的重量变为 $2x$，并继续向左走。 请参考“提示”部分的示例，以便更好地理解蚂蚁的行为。 可以证明，经过一定时间后，最终只会剩下一只蚂蚁。最初，每只蚂蚁可以随机且等概率地选择向左或向右移动，因此总共有 $2^n$ 种初始移动情况。对于队列中的每一个位置，计算该位置的蚂蚁最终存活的概率。请将答案对 $10^9+7$ 取模后输出。 形式化地，设 $M=10^9+7$。可以证明，答案可以表示为最简分数 $\frac{p}{q}$，其中 $p$ 和 $q$ 是整数，且 $q \not\equiv 0 \pmod{M}$。请输出等于 $p \cdot q^{-1} \bmod M$ 的整数。换句话说，输出一个整数 $x$，满足 $0 \le x < M$ 且 $x \cdot q \equiv p \pmod{M}$。

每组测试包含多组测试数据。第一行包含测试组数 $t$（$1 \le t \le 10^3$）。接下来是每组测试的数据。 每组测试的唯一一行包含一个整数 $n$（$1 \le n \le 10^6$），表示实验中的蚂蚁数量。 保证所有测试中 $n$ 的总和不超过 $10^6$。

对于每组测试，输出 $n$ 行。第 $i$ 行输出一个整数，表示第 $i$ 个位置的蚂蚁最终存活的概率，对 $10^9+7$ 取模。

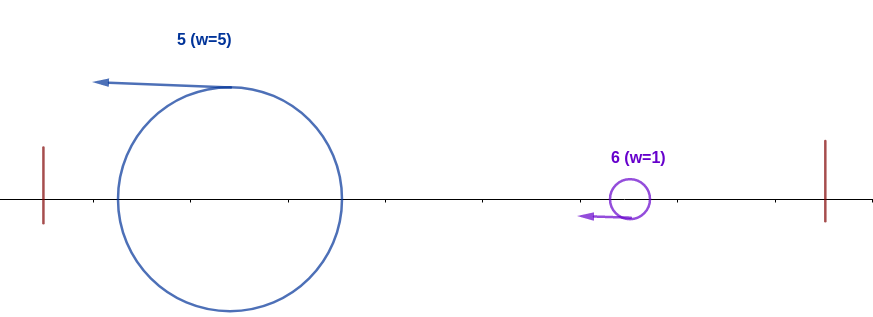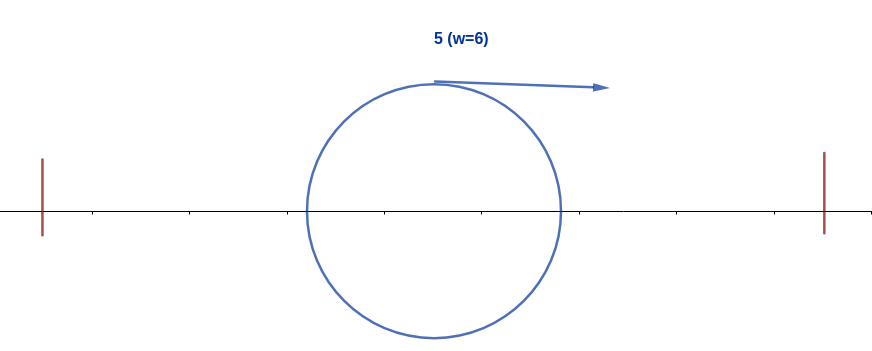以下是 $6$ 只蚂蚁在木棍上移动的示例。每只蚂蚁的移动方向用 $L$ 或 $R$ 表示。最初，蚂蚁的移动方向为 $RLRRLR$。以下是蚂蚁行为的演示： 最初，蚂蚁的位置如上图所示。 过一段时间后，编号为 $2$ 的蚂蚁（向左走）会与编号为 $1$ 的蚂蚁（向右走）相遇。两只蚂蚁重量相同，因此 $2$ 号蚂蚁会吃掉 $1$ 号蚂蚁，重量变为 $2$。同样的事情也会发生在 $5$ 号蚂蚁和 $4$ 号蚂蚁之间。 $6$ 号蚂蚁会走到木棍末端并改变方向。 之后，$5$ 号蚂蚁会与 $3$ 号蚂蚁相遇。由于 $5$ 号蚂蚁更重（重量为 $2$），$5$ 号蚂蚁会吃掉 $3$ 号蚂蚁，重量变为 $3$。 $2$ 号蚂蚁会走到木棍末端并改变方向。 之后，$5$ 号蚂蚁会与 $2$ 号蚂蚁相遇。由于 $5$ 号蚂蚁更重（重量为 $3$），$5$ 号蚂蚁会吃掉 $2$ 号蚂蚁，重量变为 $5$。 最后，当 $5$ 号蚂蚁走到木棍末端并改变方向后，$5$ 号蚂蚁会吃掉 $6$ 号蚂蚁，成为最后存活的蚂蚁。 由 ChatGPT 4.1 翻译