CF1740B Jumbo Extra Cheese 2
题目描述
Pak Chanek 有 $n$ 片二维奶酪,每一片奶酪可以表示为一个 $a_i \times b_i$ 的矩形。我们希望将它们放置在二维平面上,要求如下:
- 每片奶酪的每条边都平行于 $x$ 轴或 $y$ 轴。
- 每片奶酪的底边都在 $x$ 轴上。
- 任意两片奶酪不能重叠,但它们的边可以相接。
- 它们必须组成一个连通的整体。
注意,我们可以以任意顺序排列这些奶酪(最左边的奶酪不一定是第一片)。也可以任意旋转每片奶酪,只要满足上述所有条件。
请你求出所构造图形的最小可能周长。
输入格式
每个测试用例包含多组数据。第一行包含一个整数 $t$($1 \leq t \leq 2 \cdot 10^4$),表示测试用例的组数。接下来的每组测试用例描述如下。
每组测试用例的第一行包含一个整数 $n$($1 \leq n \leq 2 \cdot 10^5$),表示 Pak Chanek 有多少片奶酪。
接下来的 $n$ 行中,第 $i$ 行包含两个整数 $a_i$ 和 $b_i$($1 \leq a_i, b_i \leq 10^9$),表示第 $i$ 片奶酪的尺寸。
保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。
输出格式
对于每组测试用例,输出一行一个整数,表示构造出的图形的最小可能周长。
说明/提示
在第一个测试用例中,一种获得最小周长的方法如下图所示。

我们可以计算出构造出的图形的周长为 $2+5+1+1+1+1+3+1+5+1+2+3=26$。可以证明无法得到更小的周长。
考虑下面这种无效的摆放方式。
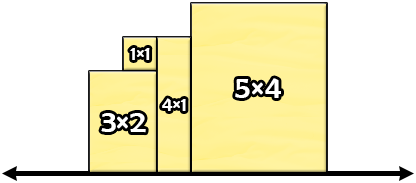
虽然上图的周长为 $24$,但它不满足题目的所有条件。$1 \times 1$ 的那片奶酪的底边没有在 $x$ 轴上。
在第二个测试用例中,一种获得最小周长的方法如下图所示。
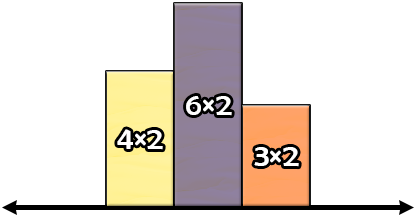
我们可以计算出构造出的图形的周长为 $2+2+2+3+2+3+2+2+2+4=24$。可以证明无法得到更小的周长。
由 ChatGPT 4.1 翻译