CF1740E Hanging Hearts

Pak Chanek 有 $n$ 张空白的心形卡片。卡片 $1$ 直接贴在墙上，而其余每张卡片都通过一根绳子挂在另一张卡片上。具体来说，卡片 $i$（$i > 1$）挂在卡片 $p_i$ 上（$p_i < i$）。 一开始，Pak Chanek 必须在每张卡片上写一个整数。他可以任意选择 $[1, 2, \dots, n]$ 的一个排列 $a$，然后将 $a_i$ 写在第 $i$ 张卡片上。 接下来，Pak Chanek 需要进行如下操作 $n$ 次，并维护一个初始为空的序列 $s$： 1. 选择一个没有其他卡片挂在它上的卡片 $x$。 2. 将卡片 $x$ 上写的数字追加到 $s$ 的末尾。 3. 如果 $x \neq 1$ 且卡片 $p_x$ 上的数字大于卡片 $x$ 上的数字，则将卡片 $p_x$ 上的数字替换为卡片 $x$ 上的数字。 4. 移除卡片 $x$。 操作结束后，Pak Chanek 会得到一个长度为 $n$ 的序列 $s$。如果 Pak Chanek 每一步都采取最优策略，最终 $s$ 的最长不下降子序列的最大长度是多少？ $^\dagger$ 序列 $b$ 是序列 $c$ 的子序列，如果 $b$ 可以通过删除 $c$ 的若干（可以为零或全部）元素得到。例如，$[3,1]$ 是 $[3,2,1]$、$[4,3,1]$ 和 $[3,1]$ 的子序列，但不是 $[1,3,3,7]$ 和 $[3,10,4]$ 的子序列。

第一行包含一个整数 $n$（$2 \le n \le 10^5$），表示心形卡片的数量。 第二行包含 $n-1$ 个整数 $p_2, p_3, \dots, p_n$（$1 \le p_i < i$），表示每张卡片挂在哪张卡片上。

输出一个整数，表示如果 Pak Chanek 每一步都采取最优策略，最终 $s$ 的最长不下降子序列的最大长度。

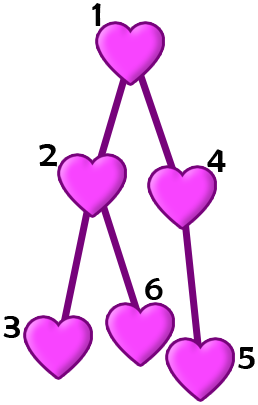
以下是第一个样例中卡片的结构示意图。  Pak Chanek 可以选择排列 $a = [1, 5, 4, 3, 2, 6]$。  设 $w_i$ 表示第 $i$ 张卡片上的数字。初始时，$w_i = a_i$。Pak Chanek 可以按如下顺序操作： 1. 选择卡片 $5$。将 $w_5 = 2$ 追加到 $s$ 末尾。由于 $w_4 > w_5$，将 $w_4$ 的值变为 $2$。移除卡片 $5$。此时 $s = [2]$。 2. 选择卡片 $6$。将 $w_6 = 6$ 追加到 $s$ 末尾。由于 $w_2 \leq w_6$，$w_2$ 保持不变。移除卡片 $6$。此时 $s = [2, 6]$。 3. 选择卡片 $4$。将 $w_4 = 2$ 追加到 $s$ 末尾。由于 $w_1 \leq w_4$，$w_1$ 保持不变。移除卡片 $4$。此时 $s = [2, 6, 2]$。 4. 选择卡片 $3$。将 $w_3 = 4$ 追加到 $s$ 末尾。由于 $w_2 > w_3$，将 $w_2$ 的值变为 $4$。移除卡片 $3$。此时 $s = [2, 6, 2, 4]$。 5. 选择卡片 $2$。将 $w_2 = 4$ 追加到 $s$ 末尾。由于 $w_1 \leq w_2$，$w_1$ 保持不变。移除卡片 $2$。此时 $s = [2, 6, 2, 4, 4]$。 6. 选择卡片 $1$。将 $w_1 = 1$ 追加到 $s$ 末尾。移除卡片 $1$。此时 $s = [2, 6, 2, 4, 4, 1]$。 $s = [2, 6, 2, 4, 4, 1]$ 的最长不下降子序列之一为 $[2, 2, 4, 4]$。因此，$s$ 的最长不下降子序列的长度为 $4$。可以证明这已经是最大可能长度。 由 ChatGPT 4.1 翻译